Mathematically Correct Breakfast  II

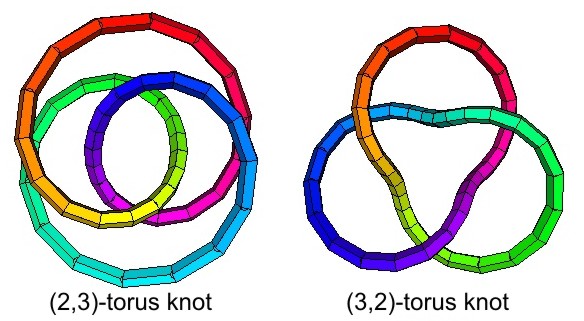
After you've mastered cutting your bagel into two linked halves, you may want to try the knotted cuts shown on this page.  They show two ways to cut a bagel into a simple overhand knot, also called a "trefoil" knot.  Above is one version, which mathematicians call "the (2,3)-torus knot toasted with cream cheese."  But it is a bit tricky, so first try the (3,2)-torus knot. They are both trefoils.

To start, you must visualize six key points. Three lie 120 degrees apart on the top of the bagel and the other three are directly below them on the bottom of the bagel.  Then a smooth spiraling line connects each top point to the other two bottom points.  For pedagogocal purposes, the construction is drawn with a marker on this bagel.  For gastronomical purposes, you are advised to just visualize the points and lines and omit the drawing step.

Follow the line with a knife, cutting halfway in, and the cut should join with the opposite cut to separate through. You can gently work it open and see the bagel is now one continuous D-shaped band that goes three times through the hole and two times around the hole. That is the meaning of the numbers in the notation "(3,2)-torus knot."

One way to convince yourself it really is a knot is to wrap a string along the surface, exactly following the path of the uncut bagel.  Then tie the ends together to form a loop. (The string does not cross itself or the cut lines.)  Can you visualize how the string forms a closed knot?

You have to break the bagel to separate it from the string. But then you will clearly see the string has an overhand knot in it, which means the bagel did as well.

---

Now, on to the (2,3)-torus knot. Again, you need to visualize six key points. As the image above shows, there are just two dots on the top, 180 degrees apart.

The other four points are visible from the bottom.  All six lie in one common plane. Each group of three lie 120 degrees apart on a circle that goes through the hole. Again, a smooth line connects each dot to the next, forming one continuous spiral. 

This version turns out to be much easier to open up.  (I think that is because it goes only two times through the hole, which is where things get tight.)

Here's the bottom view of the same bagel.  The path of the bagel goes three times around the hole and two times through it. Follow it around (or do the string thing) to convince yourself it really is an overhand knot.

Visualize the six points and the curve, so you can make the cut without drawing any lines. Then it is ready to pop into your Klein toaster and enjoy with a schmear of cream cheese! 

---