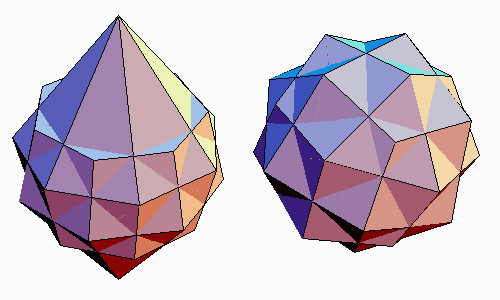
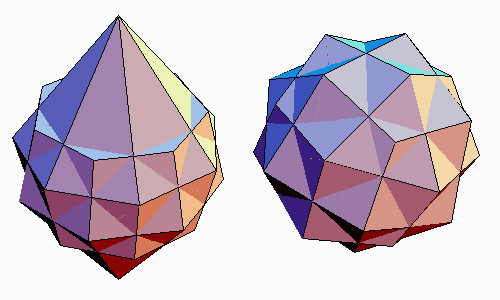
 To
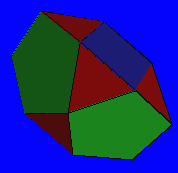
illustrate, we take an arbitrary polyhedron, the bilunabirotunda,
which consists of four regular pentagons, two squares, and eight equilateral
triangles. It is shown at left. Click on the image to view it in 3D. Clearly
its edges are not all tangent to a single sphere.
To
illustrate, we take an arbitrary polyhedron, the bilunabirotunda,
which consists of four regular pentagons, two squares, and eight equilateral
triangles. It is shown at left. Click on the image to view it in 3D. Clearly
its edges are not all tangent to a single sphere.
 However,
it is possible to construct a topologically
equivalent polyhedron which is in canonical form, shown at right. The
faces are no longer regular, but all edges are a unit distance from the
origin and tangent to a unit sphere. In addition, all the symmetry of the
original is retained, i.e., three mirror planes and three 2-fold axes.
However,
it is possible to construct a topologically
equivalent polyhedron which is in canonical form, shown at right. The
faces are no longer regular, but all edges are a unit distance from the
origin and tangent to a unit sphere. In addition, all the symmetry of the
original is retained, i.e., three mirror planes and three 2-fold axes.
The proof of the theorem does not provide a construction of the canonical form, it only tells of its existence. The paper presents an experimental algorithm which constructs the canonical form for a given input polyhedron. To illustrate the algorithm, three new self-dual polyhedra are generated. To understand their properties, we first review a few aspects of duality.
 The
dual to a given polyhedron has a face for each vertex of the original and
a vertex for each face of the original. For example, the
cube and the octahedron are mutually dual. Their edges cross at right
angles and the intersection points are on the unit sphere. For each face
of one, the other has a vertex positioned as follows: the distance of the
vertex from the origin is the reciprocal of the distance of the face from
the origin. Two vertices in the dual are connected with an edge if and
only if the two corresponding faces of the other polyhedron are adjacent.
However, the edges of a polyhedron and its dual do not generally cross
as they do here; it is only because they are tangent to the unit sphere
that this occurs.
The
dual to a given polyhedron has a face for each vertex of the original and
a vertex for each face of the original. For example, the
cube and the octahedron are mutually dual. Their edges cross at right
angles and the intersection points are on the unit sphere. For each face
of one, the other has a vertex positioned as follows: the distance of the
vertex from the origin is the reciprocal of the distance of the face from
the origin. Two vertices in the dual are connected with an edge if and
only if the two corresponding faces of the other polyhedron are adjacent.
However, the edges of a polyhedron and its dual do not generally cross
as they do here; it is only because they are tangent to the unit sphere
that this occurs.
The above is a geometric notion of duality. There is also a combinatoric or topological notion of duality, in which the geometry is ignored. Any geometrically distorted cube, e.g., a parallelepiped, is still combinatorially dual to an octahedron (or any geometrically distorted octahedron). All that is required is that we can make a mapping that associates faces of one with vertices of the other, and preserve the property that two vertices in one are connected with an edge iff the two corresponding faces of the other are adjacent. Thus geometric duality implies combinatoric duality, but not the converse.
Duality is an operation of order two --- taking the dual of the dual always gives back the original polyhedron --- so we usually speak of dual pairs of polyhedra. In a few special cases however, a polyhedron is dual to itself, i.e., it is a fixed point of the duality operator. For example, any pyramid is combinatorially self-dual, and if it is a regular right pyramid of the proper height, it is also geometrically self-dual.
If we process the hermaphrodite through our canonicalization algorithm, we get a heptagonal hermaphrodite which is geometrically self-dual, so it makes a nice compound with itself, shown at left at the top of this page.
 An
analogous construction gives the canonical form of a heptagonal
antihermaphrodite. It is composed of half an antiprism
and half a trapezohedron. Because
the antiprism and
the trapezohedron are mutually dual, the result is again self-dual,
so it also makes a nice compound
with itself, illustrated at right.
An
analogous construction gives the canonical form of a heptagonal
antihermaphrodite. It is composed of half an antiprism
and half a trapezohedron. Because
the antiprism and
the trapezohedron are mutually dual, the result is again self-dual,
so it also makes a nice compound
with itself, illustrated at right.
Canonicalizing this with our algorithm gives a tetrahedrally
stellated icosahedron in canonical form. Notice it has a very different
shape for its quadrilateral faces. Being geometrically self-dual, it makes
a nice compound with itself,
as illustrated at the top of this page, on the right. If you travel inside
it you will see that the interior, i.e., the intersection of the two, is
an attractive polyhedron composed of twenty-four
trapezoids and eight equilateral triangles. This led to one of
my sculptures, titled Yin
and Yang.