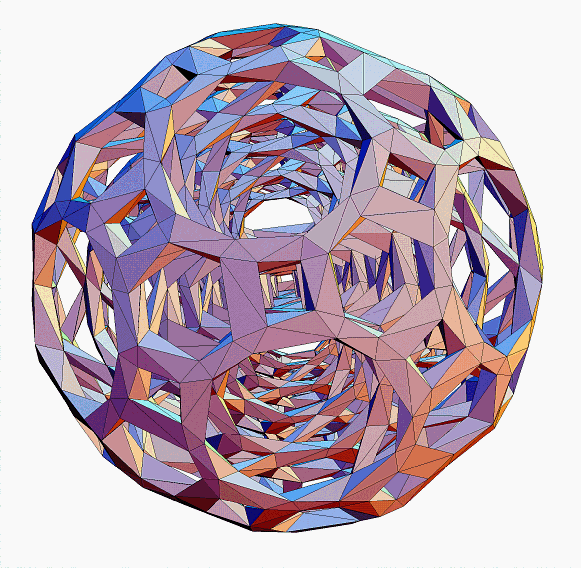ABSTRACT

Rapid prototyping refers to a wide range of state-of-the-art techniques in which a 3D design specified by a computer file is fabricated in a machine which calculates the object's cross sections, then sinters, laminates, or solidifies hundreds of very thin cross-sectional layers. I am a sculptor creating works that celebrate the beauty of geometry, but I also use rapid prototyping technologies to create interesting mathematical models. The presentation will illustrate a range of recent examples, and demonstrate some software I have written and used in this process.

There are various automated 3D assembly methods currently under development by different research groups. The three models shown in Figures 1d, 2d, and 3d are fabricated by the technique called stereolithography. A file listing a set of bounding triangles is presented to a computer-controlled laser which catalyzes a polymer-ization reaction (for each calculated cross section) at the surface of a liquid that gradually rises. After several hours of building, the fluid is drained and a plastic model is the result. While accurate and durable, the models are currently quite expensive. In the future, the cost of rapid prototyping should come down to the point where such models can be made at low cost, and they will be widely used for educational purposes.

Figure 1 shows drawings by Leonardo da Vinci, and a stereolithography model that recreates one of the forms he illustrated. Figure 2 shows an original design based on a set of topological operations: it is the expansion of the expansion of the "propellorization" of the tetrahedron, rendered in a hollow open-face manner. Figure 3 shows another novel design, this one based on six nested polyhedra in geometric progression; a general-purpose algorithm was used to wrap the edges with bounding triangles in a very efficient manner.

References [1]-[15] provide some further details about the algorithms used in each step, illustrate additional models, and discuss my related geometric sculpture.

Acknowledgment: The illustrated models were fabricated by Dr. Manfred Hofmann of RPC, Marly, Switzerland.

Figure 1a. Rhombicuboctahedron drawn with "open faces" by Leonardo da Vinci (circa 1496). This and Figure 1b are two of the sixty illustrations Leonardo prepared for Luca Pacioli's 1509 book De Divine Proportione.

Figure 1b. "Elevated rhombicuboctahedron." Leonardo and Pacioli explored nonconvex polyhedra which result from simpler forms by "elevating" them, i.e., erecting pyramids with equilateral triangles on each of their faces.

Figure 1c. Computer model of "elevated rhombicuboctahedron" provided for fabrication.

Figure 1d. Final stereolithography model, 8 cm diameter, made of epoxy resin. Small (0.01 inch) stair-steps indicate the layers.

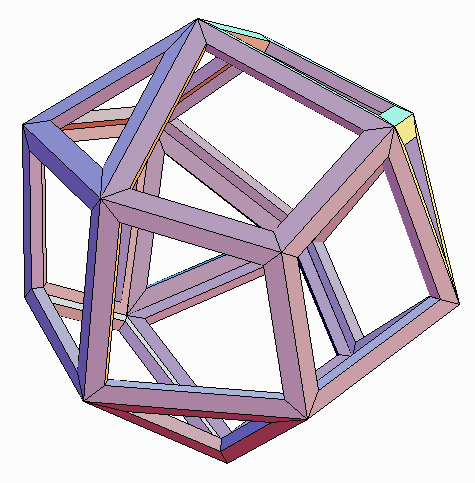
Figure 2a. "Propello-tetrahedron". This self-dual polyhedron has 16 vertices, 30 edges, and 16 faces (4 triangles and 12 kite-shaped tetragons). It is the simplest polyhedron with chiral tetrahedral symmetry, it serves as this model's "seed." In the next step is "expanded" by separating the faces and inserting a tetragon for each edge and an n-gon at each n-fold vertex. Then this expansion operation is applied again.

Figure 2b. "Expanded expanded propello-tetrahedron". This novel polyhedron has 240 vertices, 480 edges, and 242 faces (8 triangles and 234 tetragons). It is realized here in canonical form (meaning its edges are tangent to the unit sphere and the center of gravity of the contact points is at the origin) and has octahedral symmetry. It is fun to visually follow the meandering edge paths.

Figure 2c. Puncturing all the faces and creating ribs to a depth of one half of the radius produces this computer model for fabrication. It is actually in the same "Leonardo style" as Figures 1a, 1b, and 2a, but the depth parameter has been set much larger.

Figure 2d. Final stereolithography model, 4 cm diameter, made of epoxy resin. It contains a hollow space half its diameter. Close inspection reveals that it is assembled from parallel cross-sectional layers (100 per inch).

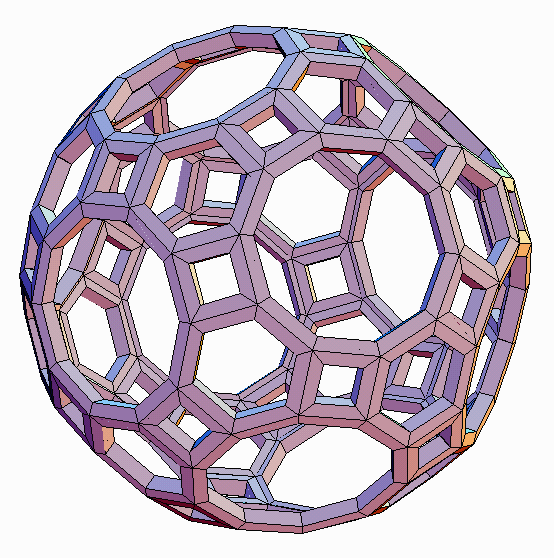
Figure 3a. Truncated icosidodecahedron (TID) rendered in the open-face style of Leonardo. This Archimedean polyhedron consists of 12 decagons, 20 triangles, and 30 squares.

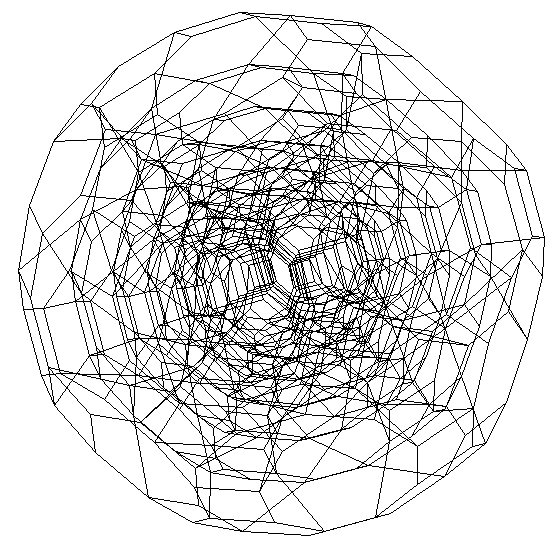
Figure 3b. Edge structure of six nested copies of the TID, each 0.8 the size of the next larger, and connected to each other by five conical helixes in each decagonal opening. 180 edges in each TID and 12 groups of 5 5-segment spirals, make 1380 segments total.

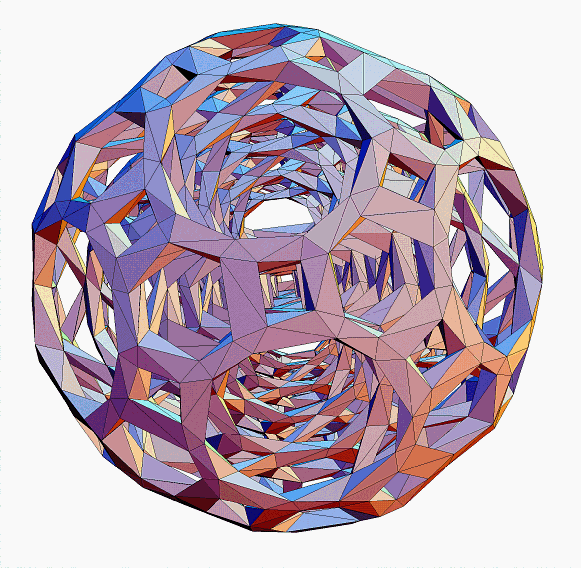
Figure 3c. By efficiently wrapping the 1380 edges in triangles, we obtain a computer model of a solid TID^6. Ready for fabrication, it bounded by 9600 triangles.

Figure 3d. Final stereolithography model, 8 cm diameter, made of epoxy resin. No other technology can produce such an exquisite crystalline object.

1. G.W. Hart, web pages, http://www.georgehart.com/
2. G.W. Hart, "Computational Geometry for Sculpture," Proc. of the Seventh Annual Symposium on Computational Geometry, ACM, Tufts University, 2001, pp. 284-287.
3. G.W. Hart, "4D Polytope Projection Models by 3D Printing," Hyperspace, (to appear).
4. G.W. Hart, "In the Palm of Leonardo's Hand," Nexus Network Journal, (submitted).
5. Craig Kaplan and G.W. Hart, "Symmetrohedra," Proc. of Bridges 2001: Mathematical Connections in Art, Music and Science, Southwestern College, Kansas, July 2001.
6. Douglas Zongker and G.W. Hart, "Blending Polyhedra with Overlays," Proceedings of Bridges 2001: Mathematical Connections in Art, Music and Science, Southwestern College, Kansas, July 2001.
7. G.W. Hart, "Loopy," Humanistic Mathematics, (to appear) 2001.
8. G.W. Hart, "Reticulated Geodesic Constructions," Computers and Graphics 24(6), 2000.
9. G.W. Hart, "Solid-Segment Sculptures," Proceedings of Colloquium on Math and Arts, Maubeuge, France, Sept. 2000. (to appear)
10. G.W. Hart, "Sculpture based on Propellorized Polyhedra," in Proceedings of MOSAIC 2000, University of Washington, Seattle, August 2000.
11. G.W. Hart, "Millennium Bookball," Visual Mathematics 2(3), and in Proceedings of Bridges 2000: Mathematical Connections in Art, Music and Science, Southwestern College, Kansas, July 2000.
12. G.W. Hart, "Zonohedrification," The Mathematica Journal, 7(3), 1999.
13. G.W. Hart, "Icosahedral Constructions," Proceedings of Bridges: Mathematical Connections in Art, Music and Science, Southwestern College, Kansas, July 1998.
14. G.W. Hart, "Zonish Polyhedra," Proc. of Mathematics and Design '98, San Sebastian, Spain, June 1998.
15. G.W. Hart, "Calculating Canonical Polyhedra," Mathematica in Research and Education, vol. 6-3, 1997.