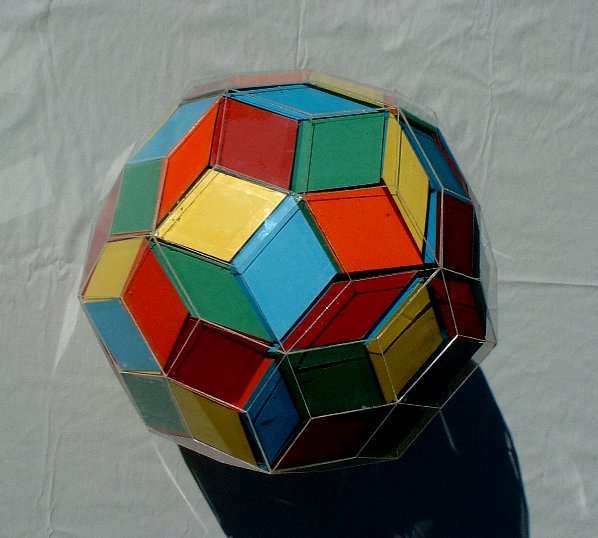 |
|
|
George W. Hart
Department of Computer Science
Stony Brook University
Stony Brook, NY 11794-4400
Abstract
The history and theory of colored zonohedral dissections is illustrated with a take-apart sculpture of a five-colored rhombic enneacontahedron that disassembles into 120 colored parallelepipeds. The components assemble in a color-matching manner to fill the interior of the 90-faced volume. The result can be viewed as a sculpture, a puzzle, or a mathematical model. Understanding the symmetry of the exterior coloring is the key to proper placement of the pieces in the interior.
1. Introduction
As a sculptor of geometric constructions, I am interested in creating visually engaging objects with an underlying mathematical richness. [12] The main result of this paper is a polyhedral sculpture, illustrated in Figure 1, which disassembles into 120 rhombohedra, as illustrated in Figure 2. The 120 parts can be assembled in a color-matched manner—red face to red face, etc.— in many ways, to build the sculpture. This is a generalization of a beautiful idea by the German mathematician Gerhard Kowalewski (1876-1950), who in 1938 published a 20-piece color-matched dissection of the rhombic triacontahedron. [17]
 |
|
|
 |
|
|
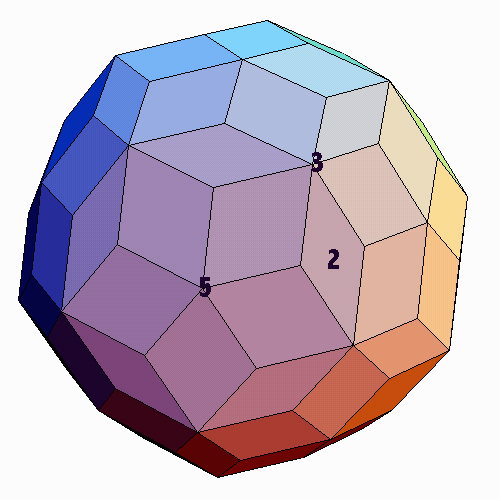
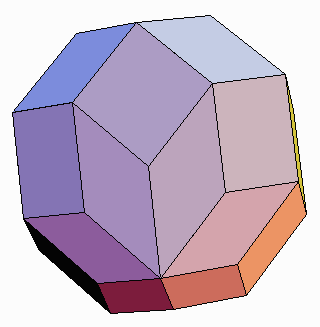
As the above figures indicate, the outer shell has the form of a rhombic enneacontahedron (RE)—a 90-faced polyhedron composed of two shapes of rhombic faces. Although this polyhedron is quite beautiful, it is not very well known. To truly understand the RE and its symmetry, it is worthwhile to make a model of it, perhaps a "Zometool" model, a computer model, or a paper model. If a Zometool construction set is available, it allows a quick assembly of a very accurate model; see [14] for instructions. A second type of very useful model is a rotating computer image. A general purpose algorithm for creating arbitrary zonohedra, including the RE and other examples below, is given in Hart [13]. But for most people, a paper model will be most appropriate.
To make a paper RE model, one needs to cut out of paper 60 "fat" rhombi
and 30 "skinny" rhombi with the same edge length. The fat rhombi have an
acute angle of about 70.53 degrees. (Or to construct it exactly, the ratio
of the diagonals is sqrt[2].) The skinny rhombi have an acute angle of
about 41.81 degrees. (The exact ratio of its
diagonals is tau2, where
tau is (1+sqrt[5]5)/2.) These 90 faces can then be taped together
using Fig. 3 as a guide. During assembly, it is useful to observe the icosahedral
symmetry axes as "landmarks" on the surface: There are 12 vertices with
5-fold symmetry, where five fat rhombi's acute angles meet. There are 20
vertices with 3-fold symmetry, where three fat and three skinny rhombi's
acute angles meet (alternating). There are also 30 points with 2-fold symmetry
(the centers of the skinny rhombi), and fifteen mirror planes. In addition,
there are 60 vertices, not symmetry points, where three obtuse angles meet.
 |
|
|
The exterior of Figure 1 is a RE shell, constructed of 90 clear "Plexiglas" (acrylic plastic) rhombi, cemented edge-to-edge. The shell is constructed in two parts that separate to allow the insertion and removal of 120 parallelepiped "blocks". There are five distinct shapes of these blocks, built from the fat and skinny rhombic shapes using five colors of acid-free card stock. The blocks can be assembled (in a great many different ways) to exactly fill the interior of the shell in a color-matching manner, e.g., red face to red face. It is interesting that one must be cognizant of a symmetric coloring for the exterior in order to fill the interior, yet one must break the symmetry of the exterior to fill the interior. The geometry and combinatorics of the block shapes and colors are detailed below in Section 4. First an introduction to zonohedra is given in Section 2 and some relevant history is given in Section 3. The problem of counting solutions is discussed in the Appendix.
2. Zonohedra
The properties of the color-matched dissection of the RE follow from the fact that it is in the special class of polyhedra called zonohedra. Three excellent references which present zonohedra at the recreational, undergraduate, and graduate levels respectively are [2], [6], and [21], and only a few key properties are given here. For the purposes of this paper, a zonohedron is defined as a convex polyhedron in which every face is a parallelogram. This is equivalent to defining a zonohedron as the Minkowski sum of a set of line segments in general position. However, the concept has evolved over time and two other, wider definitions also appear in the literature.
Zonohedral dissections are best understood by first considering the
two-dimensional analog. Figure 4 shows a "zonogon"—a centrally symmetric
2n-gon—dissected
into parallelograms. One method for its dissection starts with a parallelogram
based on any two directions then progressively expands the result in each
of the remaining directions. By the transitivity of parallelism, there
are n sets of parallel edges. The parallelograms which contain a
given edge direction form a set called a zone. Each pair of zones
crosses exactly once, which imposes significant structure on the result,
e.g., there are n(n-1)/2 parallelograms in the dissection, one for
each pair of edge directions.
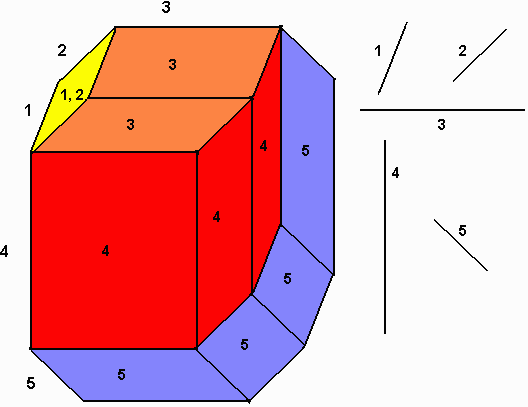 |
| Figure 4. Zonogon based on five arbitrary edge directions and lengths, dissected into 10 parallelograms. The first step uses directions 1 and 2. Then layers are added corresponding to directions 3, 4, and 5. The four cells labeled "5" form a zone. |
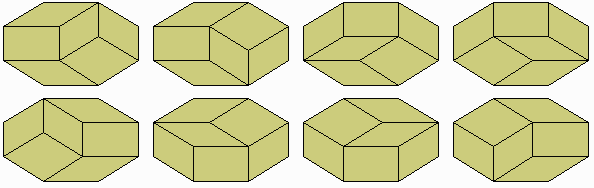
The pieces in Fig. 4 can be arranged in 62 different ways to fill the
same decagon space. The number of arrangements increases rapidly with the
size of the polygon, and Fig. 5 shows there are only eight different solutions
to an octagon. Counting the number of solutions (or equivalence classes
of congruent solutions) is a challenging open problem in combinatorial
geometry, especially in the 3D case, as discussed in the Appendix.
 |
|
counting congruent solutions as distinct. |
Generalizing, some key properties of 3D zonohedra can be gleaned from
Figure 6, which shows four zonohedra related by progressively removing
a zone of faces. Conversely, adding a zone corresponds to translation in
the new edge direction. So by starting with a parallelepiped (based on
any 3 directions) and expanding the remaining n-3 directions, zonohedra
of any complexity can be constructed based on an arbitrary set of n
edge directions. The translations of the faces at each step directly provide
a dissection of the result into n(n-1)(n-2)/6 parallelepipeds, one
for each subset of three edge directions. On the exterior, every pair of
zones crosses twice, at two opposite faces, so an n-zone zonohedron
has n(n-1) exterior faces and is centrally symmetric.
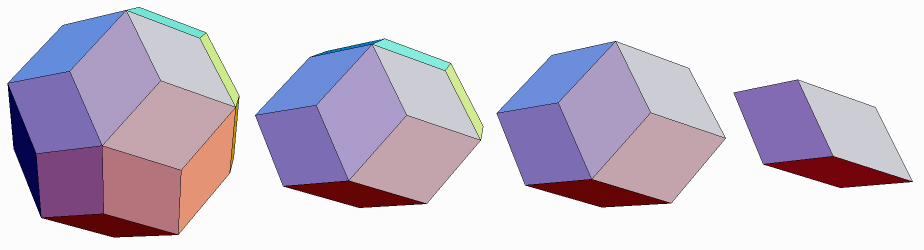 |
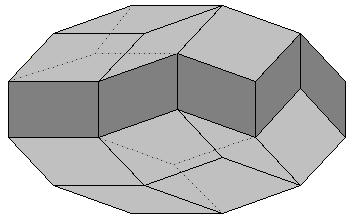
| Fig. 6. By removing one zone at a time, any zonohedron can be progressively reduced to a parallelepiped. Example: (a) rhombic triacontahedron (RT, 6 zones, 30 faces), (b) rhombic icosahedron (RI, 5 zones, 20 faces), (c) rhombic dodecahedron (RD, 4 zones, 12 faces), and (d) rhombohedron (3 zones, 6 faces). Paper models of these zonohedra can be made by taping together "golden rhombi", i.e., rhombi in which the acute angle is approximately 63.43 degrees, or the ratio of the diagonals is tau. |
More generally, as the examples in [13] indicate, one can construct beautiful zonohedra with any chosen symmetry group by first making a set of segments with the desired symmetry. The 90-faced RE (Fig. 3) arises from this construction by choosing the 10 diagonals of the dodecahedron as the edge directions. Because those directions are arranged in space with icosahedral symmetry, the resulting RE also has that symmetry.
3. History
The only parallelogram-faced zonohedra known in the classical literature, including Euclid's Elements, are parallelepipeds, which includes the special cases of rhombohedra and the cube. The next examples date to the German renaissance, when Johannes Kepler discovered the rhombic dodecahedron (RD) and the rhombic triacontahedron (RT). [15] Kepler's RD has four edge directions, i.e., four zones, which correspond to the diagonals of a cube. His RT has six zones, with edge directions corresponding to the diagonals of an icosahedron. (However, starting from a set of edge directions was not his method of construction.)
Kepler's RD is geometrically distinct from (but topologically identical to) the form shown in Fig. 6c, which is often called "the rhombic dodecahedron of the second kind" (RD2). In Kepler's RD, the rhombi's diagonals are in the ratio sqrt[2], while in the RD2, the ratio of the diagonals is tau. In Fig. 6c, at four vertices one obtuse and three acute angles meet, while in Kepler's RD the face angles meeting at any vertex are all acute or all obtuse. The RD2 is often attributed to Bilinski [3], who described it in 1960, but the form appears two centuries earlier in John Lodge Cowley's 1751 book Geometry made Easy. [5] It contains a series of paper pop-up models of polyhedra and conic sections, one of which (Plate 5, Fig. 16, labeled "Dodecarhombus") has the form of the RD2.
The earliest reference to a form closely approximating the RE is in the remarkable 1718 book Geometry Improv'd, by Abraham Sharp. Sharp was an astronomer, mathematician, and instrument maker at the Royal Observatory in London, working with John Flamseed. The book gives a new table of logarithms (to 61 places!) and presents a series of "Elegant and Beautiful" new polyhedra, especially ones with tetragonal faces. The book shows how to cut these new solids from cubes of wood. Fig, 7 is Plate II of Sharp's book, said to be "neatly engraved by his own hands", which gives a sense of the complexity of the polyhedra and the necessary cuts. One model has the topology and symmetry of the RE, but instead of rhombi, 60 of its faces are what Sharp calls "semi-rhombs", meaning they are kite-shaped. It is labeled "Fig. 43" (twice) in this plate, first centered on a 5-fold symmetry axis, and then centered on a 2-fold axis. (It is also shown a third time on Sharp's Plate III, centered on a 3-fold axis.)
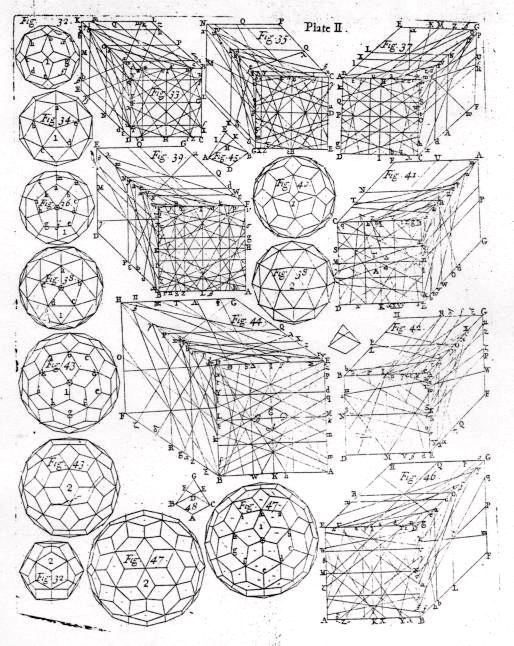 |
| Figure 7. Plate from Abraham Sharp's Geometry Improv'd, 1718. [5] At the left, near the bottom, the two figures 43 illustrate a polyhedron almost identical to the rhombic enneacontahedron. It is topologically correct, but has slightly different face angles and two edge lengths. |
Sharp explains how to cut the polyhedron out from a solid, either starting from a cube or from a rhombic triacontahedron. Curiously, he presents the necessary dimensions for the polyhedra and the cuts with 15 to 20 significant digits. In doing this he was showing off what could be calculated with his new table of logarithms, because as an astronomer and instrument maker he well knew that there was no earthly reason to work out this many significant digits; it is far beyond what is needed or usable in construction. Although Sharp was famous for the accuracy of his astronomical instruments, nothing in the text indicates whether or not he actually carried out his intricate instructions and physically constructed these polyhedra. But the accuracy of these perspective diagrams suggests that he did make models to base them on, so probably he was the first to make a model approximating the RE.
While Sharp's polyhedra emphasized tetragonal faces, they were not all parallelograms, so the polyhedra were generally not zonohedra. The first person to appreciate and define the class of zonohedra was the Russian crystallographer E.S. Fedorov. In the 1880's and 1890's he published a series of papers which included the theory underlying zonohedra, including their analysis by zones as indicated in Fig. 6, and implying their dissection into parallelepipeds. See [20] for an important distinction between Federov's original definition [8] and Coxeter's reinterpretation [2, 6], which has become the standard definition. Federov was the first to describe a rhombic icosahedron (Fig. 6b), however, he did not specifically envision the RE.
In the 1930s, Paul Donchian, an oriental rug merchant with a hobby of visualizing higher-dimensional polytopes, was the first to realize that zonohedra are the 3D shadows of higher dimensional hypercubes by linear projection. He made a range of remarkable models of polytopes and of symmetric zonohedra, which were used to illustrate Coxeter's Regular Polytopes. Some are still on display at the Franklin Institute in Philadelphia. His cardboard model, shown as Fig. 8 in Plate II of [6] is the earliest known construction of the RE.
Influenced by Donchian's models, Cyril Franklin was the first to systematically
explore "polar zonohedra", which are constructed by choosing n equal-length
edge directions symmetrically around an axis, like the ribs of a half-open
umbrella. [9]. An example of a six-zone polar zonohedron is shown in Fig.
8. Note how it is topologically different from the RT (Fig. 6a), which
also has six zones and 30 faces, but no 6-fold vertices. In fact these
are just two of four distinct topological structures possible for 6-zone
zonohedra. There is only one possible topological form—equivalent to the
polar zonohedron—for the case of 3, 4, or 5 zones.
 |
|
|
The insight that there is a correspondence between these possible topologies and arrangements of lines in projective space is due to Coxeter [7]. In the 1940's, H.S.M. Coxeter revised W.W. Rouse Ball's classic Mathematical Recreations and Essays [2], adding a new chapter on polyhedra illustrated with Donchian's models. In that chapter he discusses zonohedral dissections, and in particular points out that any n-zone zonohedron can be dissected into n(n-1)(n-2)/6 parallelepipeds, one for each triple of generating directions.
In 1954, the architect R. Buckminster Fuller, always attuned to the
aesthetics of geometric forms, constructed what is undoubtedly still the
record-holder for largest RE. It is a hemispherical dome, shown in Fig.
9 with Fuller inside it. However most of Fuller's domes were triangulated
and not zonohedral.
 |
| Figure 9. Dome by R. Buckminster Fuller in form of RE, Washington University, St. Louis, 1954. (Image courtesy of The Estate of R. Buckminster Fuller.) |
In the 1970's, another architect and dome builder, Steve Baer, explored the systematic use of zonohedra as the basis of architectural forms. [1] He invented a system which allows the easy assembly of such models and called it Zometool, contracting "zonohedron dome" to "zome". See [14] for detailed instructions for all the zonohedra illustrated in this paper. Baer's Zome Primer discusses the dissection of the RE into 120 parallelepiped blocks. It gives the geometric information necessary for constructing the individual blocks, but does not consider coloring issues.
4. The Colored RE Dissection
The coloring of a zonohedral dissection is the idea of the German mathematician
Gerhard Kowalewski, who was inspired by a well-known color-matching cube
puzzle called "MacMahon's cubes". In 1938 Kowalewski published a lovely
monograph about a color-matching dissection of the rhombic triacontahedron
into 20 parallelepiped pieces. Fig. 10 shows a disassembled model. There
are two shapes of pieces, both made using only the 63.43 degree angle rhombus
of Fig. 6. Details are given in [17], but briefly: for each of the 10 ways
to choose three colors from a palette of five colors, make a pair of rhombohedra.
For example, if the five colors are A, B, C, D, and E, one of the ten combinations
is to make a block with two opposite faces colored A, two opposite B's,
and two opposite C's. One such block will have the "acute" shape shown
in Fig 6d, in which three acute angles meet on the 3-fold symmetry axis.
The other of each pair will be an "obtuse" rhombohedron, almost flat, with
three obtuse angles meeting on the 3-fold symmetry axis.
 |
|
|
These 20 different pieces can be joined in a color-matching manner to form a rhombic triacontahedron. (There are 320 distinct solutions; see Appendix.) In every solution, the exterior of the RT is symmetrically colored such that two faces receive the same color iff they are either parallel or perpendicular. This is the well-known five-coloring of the RT based on viewing it is the intersection of the dodecahedral compound of five differently colored cubes. [6]
There are two scenarios for making a puzzle from a colored zonohedral dissection. One might be given the exterior coloring to follow, e.g., with a hollow colored shell to fill as in Fig. 10, or one might be free to choose any exterior coloring, e.g., with an uncolored shell as in Fig. 2. Kowalewski's puzzle is more challenging with an uncolored shell. If one starts assembling pieces by making local color matches, but unaware of the final symmetric coloring, one is likely to build what appears to be a partial solution, but which cannot be extended into a complete solution. But with a colored shell as a guide, it is easy to check that each added piece has its face colors in agreement with the parallel faces of the shell.
Coloring the RE is a natural extension of Kowalewski's RT idea, but more complex because there are 120 pieces of five shapes made from two types of rhombi. First consider the coloring aspect. Generally, an n-zone zonohedron's faces come in n(n-1)/2 opposite pairs, so we may use up to that many colors to paint a zonohedron's faces and maintain the property that opposite faces receive the same color. Choosing fewer colors allows a repetition of colors in a symmetric pattern, e.g., Kowalewski used 5 colors rather than 15.
Given any dissection of such a colored zonohedron, it is straightforward to extend the exterior coloring inwardly in a consistent manner to the blocks of the dissection. The dissection becomes color-matched automatically if we choose each face of each block in the interior to be the same color as the two exterior faces with which it is parallel. This rule forces opposite faces in each block to share a common color. The coloring is a function of parallelism and is unchanged by translation, so if the blocks are constructed for one color-matched dissection they automatically are suitable for any of the other dissections with the same exterior coloring. This is because the n(n-1)(n-2)/6 parallelepiped blocks each correspond to one triple of generating directions, so the many solutions for a zonohedral dissection differ only by the translation of the component blocks.
Choosing the number and pattern of colors is an interesting design problem.
I chose five colors for the RE after experimenting with a variety of different
colorings. The 30 skinny rhombi of the RE are in the planes of five cubes,
so can be colored in the same way as the five-colored RT. Figure 11 shows
once the pattern chosen for each color. At each end of each skinny rhombus
a fat rhombus is assigned the same color. Five rotated copies of this pattern,
in five different colors, exactly cover the RE.
 |
| Figure 11. RE with one orbit of color shaded. Five such orbits, in five different colors, exactly cover the surface. This pattern was chosen for the sculpture shown in Fig. 1. |
Working inward from this pattern, the inventory of required parts is determined by considering each subset {x, y, z} of three directions from the ten edge directions. The colors and shapes of the faces in the exterior xy, xz, and yz planes determine one interior block. With a model in hand (Zometool and/or paper) to read off the shapes and colors, one can work out that the 120 components fall into the following five groups:
5. Conclusions
An attractive, symmetric five-coloring of the rhombic enneacontahedron's faces is the basis for its dissection into 120 three-colored parallelepipeds. A large hands-on sculpture based on this construction has been created from card stock and plastic. The components assemble in a color-matching manner to fill the interior in a very satisfying manner, and the number of solutions is more than can be counted at present. These principles may be applied to create other disassemblable colorings of other zonohedra.
Appendix. Counting the Number of Dissections
The question of how many distinct solutions there are to the RE dissection is an instance of the well-studied, but very difficult "zonotopal tiling problem". It is still open, despite significant recent progress on similar, simpler problems using oriented matroid theory [4]. A recursive method of counting the number of different ways in which the pieces of a zonohedron dissection may be re-assembled is sketched here, but the number of solutions grows hypergeometrically, so this method is too slow to provide an answer for the RE.
Consider first the 2D case, in which a 2n-gon is dissected into
n(n-1)/2
parallelograms. For n=4, there are 8 ways of dissecting an 8-gon
into 6 parallelograms, as illustrated in Fig. 5. But the number of such
dissections increases very rapidly with n. Table 1 shows that for
n=9 the number exceeds 108. These numbers, from Knuth
[16, p. 35], are relevant because of an interesting correspondence between
sorting networks, pseudo-line arrangements, and zonogon dissections. [16]
shows that the rate of growth of the 2D problem is O(2^n^2), and
provides these calculated values for small n. This data was valuable
as an independent check on our software.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 1. The number of ways to dissect a 2n-gon into n(n-1)/2 parallelograms.
In the 2D case, knowing the number of sides of the polygon determines
the problem completely. But in the case of 3D dissections there are different
topologies possible when n>5. There are 4 topologically distinct
6-zone zonohedra and 11 distinct 7-zone zonohedra. So any method that enumerates
3D solutions must be sensitive to the edge directions, unlike the 2D case,
which can be approached in a much faster purely combinatorial manner. Table
2 shows the number of solutions for n-zone polar zonohedra
according to the author's software for enumerating solutions. However,
the number of solutions depends on the topology (but not the geometry),
e.g., among the 6-zone zonohedra, there are 148 solutions for the polar
zonohedron (Fig. 8), yet 160 solutions for the RT (Fig. 6a).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 2. The number of ways to dissect an n-zone polar
zonohedron into n(n-1)(n-2)/6 parallelepipeds.
These are counts of the number of ways to fill a fixed, uncolored shell. The number of distinct solutions would be reduced if one instead counts equivalence classes of congruent solutions. Or the number could be increased if the same set of pieces can be assembled into non-congruent colorings of an uncolored shell. For example, in Kowalewski's RT puzzle, there are two ways to five-color the exterior. This is because the icosahedral rotation group is isomorphic to just the even permutations of five colors, so any odd permutation of the colors gives a new coloring not obtainable by a rotation. If one is given a 5-colored RT shell to fill, there are 160 ways to assemble the pieces in it. But if one is given an uncolored shell, there are two solvable colorings for the exterior, making 320 solutions all together.
Figure 12 gives a sketch of the central idea of the algorithm, using
the 10-gon as a 2D analog. It is not difficult to show that after a zonal
"slice" is selected the two separated portions of the remainder can be
solved independently, i.e., any remaining piece will fit on just one side
or the other of the slice, not both. So the number of solutions to the
two subproblems can be counted separately and multiplied. This allows a
considerable speedup over enumerating every solution individually, though
it is still not fast enough.
 |
| Figure 12. 10-sided Zonogon dissected into slice (darker) and two regions (lighter) which can be solved independently. Of the 62 dissections of the 10-gon, four share this slice and are indicated in the figure. The dotted lines show there are 2 solutions for the top region and two for the bottom, multiplying to give 4 solutions for this slice. The algorithm sums these products over the different ways of making the initial slice, invoking itself recursively in the two regions. |
The approach implemented keeps a list of faces that represent the boundary to be filled, which is initially all the faces of the zonohedron to be dissected. All possible slices for the first zone are found in a depth-first search, as follows. Choosing any boundary face in the first zone, the possible blocks adjacent to it are determined using a set of -/0/+ coordinates of an oriented matroid. Each such block is first checked to ensure it is not parallel to any block already used. Then it is checked to see that it does not intersect the boundary to be filled, using a standard linear programming technique to efficiently search for a separating hyperplane between the block and blocks selected earlier. If the block is acceptable, the boundary is updated by XORing it with the block's faces. These steps are repeated until a "slice" of blocks with edges in the first zonal direction is filled in. This separates the remaining space into two smaller independent problems—one on each side of the slice. For each such slice, the two smaller problems are solved recursively, and the product of the two numbers of sub-solutions is added in to the number of solutions for this problem.
The software is written in Mathematica and works generally for the projection of an n-dimensional hypercube onto an m-dimensional subspace. It is not optimized for speed, so with some programming effort the program could be sped up by a significant multiplicative factor. But there is little hope of counting the RE solutions without a new approach. This remains an interesting open problem.
References
[2] Ball, Walter William Rouse, revised by H.S.M. Coxeter, Mathematical Recreations and Essays, New York, 1938; 11th ed., 1960, (Dover reprint, 1987).
[3] Bilinski, S. "Über die Rhombenisoeder", Glasnek Mat. Fiz. Astronom. Drustvo Mat. Fiz. Hrvatske (series 2) 15, 1960, pp. 251-262.
[4] Björner, Anders, et al., Oriented Matroids, Cambridge, 1999.
[5] Cowley, John Lodge, Geometry made Easy, 1751.
[6] Coxeter, H.S.M., Regular Polytopes, Macmillan, 1963, (Dover reprint, 1973).
[7] Coxeter, H.S.M., "The Classification of Zonohedra by Means of Projective Diagrams," in Twelve Geometric Essays, S. Illinois U. Pr., 1968, (reprinted as The Beauty of Geometry: Twelve Essays, Dover, 1999).
[8] Fedorov, E. S., Symmetry of Crystals, translated by David and Katherine Harker, American Crystallographic Assoc., 1971.
[9] Franklin, Cyril H.H., "Hypersolid Concepts, and the Completeness of Things and Phenomena," Mathematical Gazette, 21, Dec. 1937, pp. 360-364.
[10] Fuller, R. Buckminster and Robert Marks, The Dymaxion World of Buckminster Fuller, Southern Illinois Univ. Pr., 1969, (Anchor Books reprint, 1973).
[11] J. E. Goodman and J. O'Rourke, eds., Handbook of Discrete and Computational Geometry, CRC Press, 1997.
[12] Hart, George W., "Geometric Sculpture," http://www.georgehart.com
[13] Hart, George W., "Zonohedrification," Mathematica Journal, Vol. 7 no. 3, 1999.
[14] Hart, George W., and Henri Picciotto, Zome Geometry: Hands-on Learning with Zome Models, Key Curriculum Press, 2001.
[15] Kepler, Johannes, The Harmony of the World, 1625, (transl. E.J. Aiton, A.M. Duncan, and J.V. Field, 1997, American Philosophical Society).
[16] Knuth, Donald, Axioms and Hulls, Lecture Notes in Computer Science 606, Springer-Verlag, 1991.
[17] Kowalewski, Gerhard, Der Keplersche Korper und andere Bauspiele, Koehlers, Leipzig, 1938. (In English translation as Construction Games with Kepler's Solid, tr. David Booth, Parker Courtney Press, 2001.)
[18] Senechal, M., Quasicrystals and geometry, Cambridge, 1995.
[19] Sharp, Abraham, Geometry Improv'd, London, 1718.
[20] Taylor, Jean E., "Zonohedra and Generalized Zonohedra," American Mathematical Monthly, February 1992, pp. 108-111.
[21] Ziegler, Gunter M., Lectures on Polytopes, Springer-Verlag,
1995.