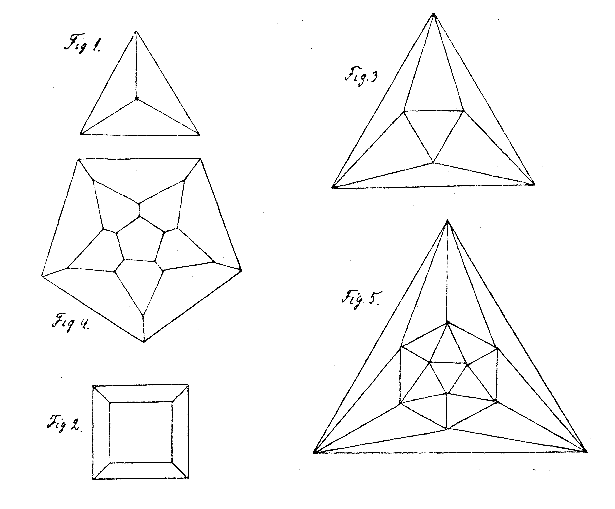
Figures 1-5. "Schlegel diagrams," from [26], of the five Platonic solids:
1) tetrahedron, 2) cube, 3) octahedron, 4) dodecahedron, 5) icosahedron.
4D Polytope Projection Models by 3D Printing
George W. Hart
Department of Computer Science
State University of New York at Stony Brook
Abstract
The author's experience using "3D printing" technology for producing physical models of four-dimensional objects such as the 120-cell is summarized. For background and comparison, previous mathematical models of the 120-cell are reviewed first.
1. Introduction
Three-dimensional projections of four-dimensional polytopes are valuable for teaching and self-education about higher-dimensional geometry. Experience shows that physical models—real 3D objects—are especially useful for developing intuition and understanding about 4D polytopes. A variety of physical modeling techniques are possible, with three popular materials being paper (or cardboard), wire (or wire and string), and Zometool (a plastic construction set). This paper illustrates a new 3D-printing technique that I expect will supplant these traditional materials for a wide range of mathematical modeling applications.
3D-printing allows the creation of models that are very compact, intricate, accurate, and portable. This state-of-the-art technology involves the automated (robotic) assembly of physical models by assembling very thin cross-sections calculated from the designer's computer file describing the structure to be built. This new technology will have applications in the creation of all types of educational 3D models, e.g., polyhedra, topological or algebraic surfaces, molecular models, crystal structures, anatomical models, etc. However, this paper focuses on geometric models related to the 120-cell, and its family of truncations and expansions. This example is featured because the author considers it one of the most beautiful geometric objects—yet it is not widely enough known, in part because of the lack of models.
Software presentation of geometric structures, e.g., interactively rotating images on a computer screen, have a valuable and growing role in modern education. (Search the internet for "120-cell" to locate several fine examples.) However there has been and will always be a role for physical 3D models. In the heyday of physical mathematical models, from the 1870s to World War I, universities were proud to boast of their educational models. The German geometer Felix Klein was a strong advocate of models in mathematics education reform, and American universities that emulated the German system purchased German-made models such as surfaces and polyhedra. For an excellent overview of this period, see Kidwell [18], but she does not discuss models for illustrating higher-dimensional geometry. Fischer [6] illustrates a wide range of mathematical models from this period, including stick models of 4- and 5-dimensional hypercubes (in the collection of the Palais de la Decouverte, Paris), but nothing as complex as the 120-cell. Mueller [21] emphasizes the sense of wonder that such mathematical models can excite in the viewer.
To understand projection models, first consider the "Schlegel diagrams" of Figures 1-5. [26] These show the five Platonic solids, each projected from 3D to 2D. These can be understood as shadows, from a nearby point light source, of the edges of the polyhedra. The geometry of the 3D lengths and angles is distorted in the projection, e.g., a square may project into a trapezoid, but all the topological properties are preserved. In each case, the outer boundary must be considered as one of the faces of the polyhedron, divided into regions representing the remaining n-1 polygons. The outer polygon can be thought of either as overlaying all the other faces or as an inside-out infinite polygon, filling the remainder of the plane. For example, in the cube's shadow at lower left, one must see six tetragons, not five, to understand that there are three squares meeting at each vertex. Figures 1-5 show "perspective projections," meaning the shadow-producing light source is nearby. From a light source infinitely distant, "Orthographic projections" result, in which the shadows of some edges will cross.

Figures 1-5. "Schlegel diagrams," from [26], of the five Platonic solids:
1) tetrahedron, 2) cube, 3) octahedron, 4) dodecahedron, 5) icosahedron.
By "dimensional analogy" one can understand the structure of 4D polytopes from their perspective and orthographic projections into 3D space. Section 2 of this paper presents a history of 3D projection models of 4D polytopes, illustrating a range of examples known to this author. Then in Section 3, new 3D printing technology is described and several models are presented starting with my first geometric experiments and working up to intricate 4D models.
2. Some physical models of the 120-cell and other 4D polytopes:
The history of 4D Euclidean geometry is documented in a number of references. [4, 2, 28, 30] In 1852 Ludwig Schläfli discovered the six regular convex 4D polytopes: the 5-cell, 8-cell, 16-cell, 24-cell, 120-cell, and 600-cell. He also discovered four of the ten non-convex ones. But higher dimensional geometry was not a popular field of mathematics then, and his results were not appreciated. Also, Schläfli worked algebraically; the paper has no images of any sort which might have helped readers appreciate it. In 1858 and 1860 his paper was partly published in English translation by Arthur Cayley. However, it was only published in its entirety posthumously, in 1901. [24] In the 1880s, the topic became popular and many mathematicians, unaware of Schläfli's work, were competing to discover the higher-dimensional regular polyhedra.
Stringham [32] was the first to independently rediscover the six regular
convex 4D polytopes. His 1880 paper includes images of what appear to be
paper models. Figure 6 shows one of his figures that illustrate the structure
of the 120-cell. Its 3D projection can be built by choosing one dodecahedron
to be at the center and surrounding it by layers of 12, 20, 12, 30, 12,
20, 12, and 1 dodecahedra, totaling to 120. Stringham illustrates four
stages in this process. Figure 6 is the result after three layers, i.e.,
an assemblage of 45 dodecahedra. There are also analogous images for the
structure of the other regular 4D polytopes.
 |
|
|
In 1883, Victor Schlegel constructed accurate projection models of the six regular 4D polytopes, made from brass wire and silk thread. [25] These were first exhibited at the 1884 meeting of the Society of German Naturalists. This was the height of the educational mathematical model period, and 4D polytopes became mainstream enough that physical models of the six were soon commercially available through mathematical supply catalogs. Schlegel's designs were sold first by Ludwig Brill of Darmstadt, and then by his firm's successor, Martin Schilling of Leipzig. [23; 28, p. 191] Schlegel's five-page instructional brochure uses Figures 1-5 to explain the models by means of dimensional analogy. [26] Examples of these wire and string models of the 5-, 8-, 16-, and 24-cell are on display at the University of Göttingen Mathematics Department. The only surviving examples I have been able to locate of the German 120-cell and 600-cell models are in the mathematics collection of the Smithsonian Museum in Washington, DC. However at this time they are in storage, missing their strings, and in need of conservation.
Sommerville [29] gives a mathematical description of these models:
 |
|
|
Horsburgh's 1914 Handbook of the Napier Tercentenary Celebration records that projections of the six regular 4D solids by J.E.A. Steggall were on display. Described only as "a representation, with the dissection of certain parts," their material is not specified. [17] It also records the projection model of the 600-cell made of brass wire and silk by D.M.Y. Sommerville. In contrast to Schlegel's cell-centered projections, this projection is centered on a vertex, as detailed in [29]. There is no image, but the description in [17] concisely explains the construction:
 |
|
|
Various individuals, captivated by the geometric beauty of these forms, have independently made 120-cell models for their own gratification or edification. Several 5-foot welded stainless steel models constructed in the 1990s by Marc Pelletier are most impressive. Yuro Otobe has constructed a series of soldered and painted steel wire models (up to 20 cm in diameter) since about 1980. They have been presented in seven previous issues of Hyperspace and are on display at the museum of the Mathematical Institute of the University of Tokyo. Paper (or cardboard) is a popular, inexpensive modeling material, so it is likely that many people have used it for polytope projection models in addition to Figures 6 and 7 above. A notable example is that Koji Miyazaki constructed beautiful color paper models of the 120-cell illustrated in [20, p. 74, 95].
In 1970 Steve Baer designed and produced a geometric modeling set called
"Zometool" with plastic nodes and wooden struts [1]. Marc Pelletier discovered
(when 17 years old) that the lengths and directions allowed by this kit
permit the construction of accurate models of the 120-cell and related
polytopes. The kit went out of production however, until 1992, when it
was redesigned in a plastic version that can be used to make an extremely
wide range of mathematical models. [35, 15] In particular it is capable
of making models of the 120-cell and 600-cell, and their family of truncations
and expansions.
 |
|
|
Figure 9 shows a Zometool model of the truncated 120-cell, a 4D polytope consisting of 120 truncated dodecahedra and 600 regular tetrahedra. Instructions for its construction are given in [15, p. 211]. This is one of many "Archimedean" polytopes discovered by Alicia Boole Stott and first described in her 1910 paper [31]. She was a daughter of George Boole, untrained in mathematics, and has a fascinating story outlined in [4, p. 258]. This 1.5 meter model was constructed in a student workshop led by the author at Mathcamp 2000 in Vancouver. [19] (The students had made a Zome 120-cell model on the previous day, in preparation for this larger project.) In this projection, it produces a stunningly beautiful 3D form with 10-sided passageways piercing it in six different directions. In the several hours required for its construction, the students gained a significant appreciation of the geometric issues. This is also an excellent social, engineering, and visual experience. However, making large Zome models of several related polytopes would require excessive time.
3. Models produced by 3D Printing
In this context, I set out to make new models of 4D polytopes using
state-of-the-art rapid prototyping technologies. There are various automated
3D assembly methods currently under development by different research groups.
[3] What they have in common is that the 3D design specified by a computer
file is fabricated in a machine which sinters, laminates, or solidifies
hundreds of very thin cross-sectional layers. One early technique ("laminated
object manufacturing") uses a computer-controlled knife or laser to cut
sheets of paper, which are automatically stacked and glued to each other
to make a wood-like material. The "stereolithography" technique directs
a laser that catalyzes a polymerization reaction for each cross section
at the surface of a liquid that gradually rises, resulting in a plastic
model after the fluid is drained. The Fused Deposition Modeling (FDM) technique
is effectively like a "hot melt glue gun" at the end of a robotic arm,
which builds a plastic model in the air. Selective laser sintering (SLS)
uses a laser to sinter wax or metal dust in a chamber to which is added
a new (thin) layer of dust after each cross section. When complete, the
loose dust is vacuumed away and the hardened model remains. The technology
I have used the most is "3D printing", like this last, but the dust is
plaster and the mechanism of an ink-jet printer is used to print the cross
sections with water. Developed by the Zcorp corporation, this technique
is promoted as relatively inexpensive. [34] Unless otherwise stated, the
models below were produced by Zcorp and are each about 8 cm in diameter.
Typically, several hours are required to build each.
 |
|
|
 |
|
|
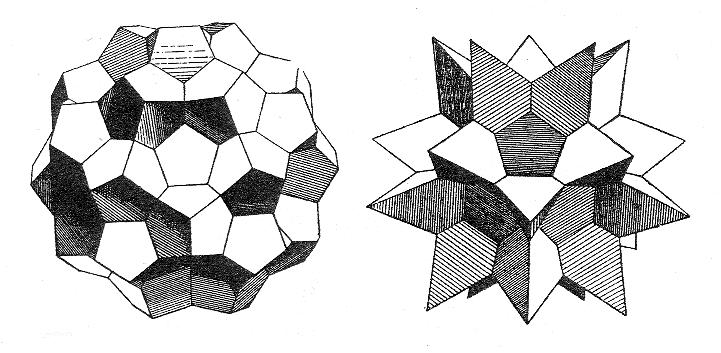
To familiarize myself with this technology, the first two models that I made were solid polyhedral compounds with icosahedral symmetry. Figure 10 shows the compound of five truncated tetrahedra, derived by truncating all the tetrahedra of the standard compound of five regular tetrahedra inscribed in a dodecahedron. Figure 11 shows the uniform compound of six pentagonal prisms. Each prism has its 5-fold axis aligned with one of the 5-fold axes of the icosahedral symmetry group, and is rotated on its axis to a position intermediate between that of the two opposite faces of a dodecahedron. Described in a 1976 paper by John Skilling, [27] as far as I know these two compounds had not been made previously in paper or any other media. However, they could straightforwardly be made in paper, and instructions for Zometool models of both are available on my web pages [9].
After gaining experience with the technology, file formats, and other
production issues, I decided to try hollow models with a thin shell, which
would be more difficult to produce by any other technique. Figure 12 shows
an original form, which I call the snub truncated icosahedron. Like
the snub Archimedean solids, i.e., the snub cube and snub dodecahedron,
this form is derived by inserting a chiral structure of triangles between
the faces of a simpler polyhedron. In this case, the simpler polyhedron
is the truncated icosahedron, consisting of 12 regular pentagons and 20
regular hexagons. However, the result is not an Archimedean solid and the
snub triangles must differ slightly from equilateral. I chose an open-faced
edge model, in the style of Leonardo da Vinci. The result is a very light
structure, like an eggshell.
 |
|
|
Having gained better insight into the technology, and a sense of how
thin the struts can be, I felt ready to make open models with internal
structure. Figure 13 shows a 10-cm form with five nested concentric spheres.
Artistically, I was paying homage to the long tradition of "Chinese Balls"
in which ivory spheres are turned on a lathe and then carved, to produce
intricate concentric forms. [16] For my structure, I chose a form which
is the 31-zone zonohedron based on the directions of the rotation axes
of the icosahedral symmetry group. Each of the five layers has the same
structure as the outer, most visible, orb: there are 30 large 12-sided
oval openings, 12 smaller 10-sided openings, 80 irregular hexagonal openings,
and 120 small rectangular openings. Oval "corkscrew spirals" in the 12-sided
openings connect the layers with each other. I consider this a sculpture
rather than a mathematical model, although that distinction can be difficult
to draw. It is titled Deep Structure.
 |
|
|
In the underlying mathematical structure of Figure 13, there are 4080 line segments positioned in space. However, the computer format for specifying 3D printing requires a volume bounded by a list of triangles. So a significant part of my work was to develop an efficient general purpose algorithm that creates a triangulated surface surrounding an arbitrary set of line segments. The algorithm is described in [13]. For producing the result in Figure 13, there are 27214 triangles altogether, a very low number for such a complex, high-genus structure.
The same algorithm can produce suitable triangulated structures when
given a list of edges for a projected polytope. The necessary vertex coordinates
and edge lists for polytope projections are relatively straightforward
to produce. [4, 33] Figure 14 shows a virtual model of the 120-cell. This
is a standard orthogonal projection along a line that connects the centers
of opposite cells. However, as a sculptor, I am interested in visually
interesting effects, so for my first 3D model, I made a small variation
to the algorithm, producing the chiseled sculptural form of Figure 15 rather
than the mathematical model in Figure 14. Its blue color results from a
dye added to the plaster. Again, as I consider this a sculpture, I give
it a name: the Five-Legged-Bee Hive. It was exhibited at the art
display of the International Colloquium on Mathematics and Art, at Maubeuge,
France, in September, 2000. I more recently gained access to a FDM machine,
and produced the 8cm plastic model shown in Figure 16.
 |
|
|
 |
|
|
 |
|
|
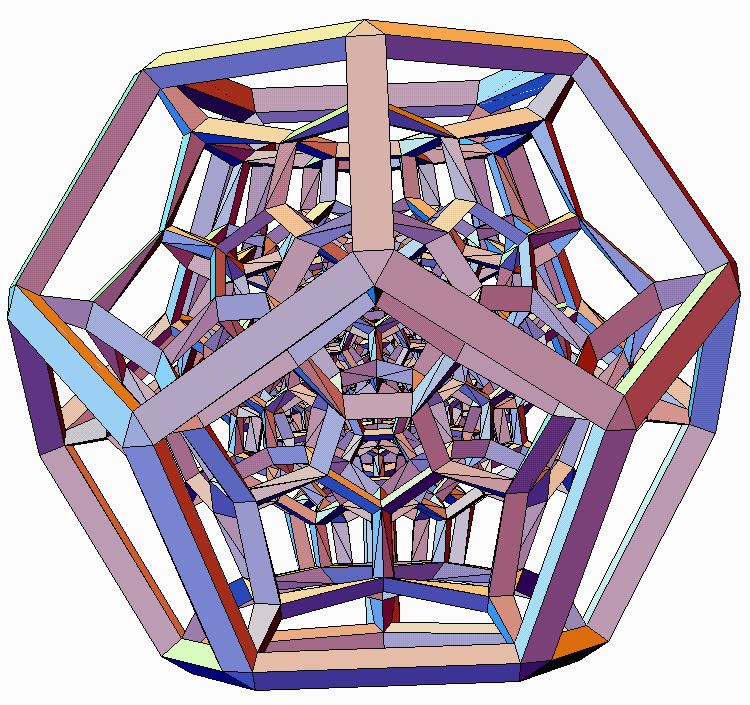
Next, Figure 17 shows a perspective projection of the 120-cell, a 3D
analog to a 2D "Schlegel Diagram". For visual interest, the strut thickness
was made to vary smoothly from thin at the center to thick at the exterior.
Because of its intricacy, a different technology was employed when building
it. Figure 18 shows a wax model, produced by a Sanders machine [22]. This
design was worked out in discussions with Carlo Sequin, who also paid for
its production cost. The 3D printing is 5 cm across, executed and photographed
by Bathsheba Grossman. [8]
 |
|
|
 |
|
|
Figures 19 and 20 show models of two 4D Archimedean polytopes discovered
by Alicia Boole Stott. [31] Both are orthogonal projections, built from
a translucent epoxy by the stereolithography process using a 3D Systems
rapid prototyping machine. [36] The first shows the "truncated 120-cell,"
which consists of 120 truncated dodecahedra and 600 tetrahedra. It is derived
by truncating the 600 vertices of the 120 cell. A Zome model of it is shown
in Figure 9. The second is the "rectified 120-cell," which consists of
120 icosidodecahedra and 600 tetrahedra. It is derived by truncating the
120 cell further, to the edge midpoints.
 |
|
|
 |
|
|
4. Conclusions
As a sculptor and applied mathematician, I am interested in understanding and creating beautiful geometric forms and then presenting them to the public. See [9-13] for a range of my creations. For each object, I must choose materials that are visually and structurally appropriate. When the underlying structures are of an intricate four-dimensional nature, this offers a difficult challenge. Following on my study of previous techniques, I have come to appreciate the impressive capabilities of rapid prototyping techniques for realizing forms that would otherwise remain trapped in the imagination.
Beyond sculpture, models of 4D structures are of established educational
value. In the past, paper, wire, and Zometool have allowed the construction
of useful teaching models. To this list I now recommend that rapid prototyping
techniques be considered for such geometric education purposes. A 120-cell
model such as Figure 16 is conveniently passed around in a classroom, held
in the hand, rotated, studied, and compared to a different model in the
other hand. Although relatively expensive at present, the costs are decreasing.
In the future, I expect, all schools will have 3D printing capability.
Teachers will easily be able to produce a variety of stimulating models
to be used for lessons and to stock a "cabinet of curiosities" which can
excite a sense of wonder about mathematics.
References
[2] Thomas F. Banchoff, Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, W. H. Freeman, 1990.
[3] Marshall Burns, Automated Fabrication: Improving Productivity in Manufacturing, Prentice Hall, 1993.
[4] H.S.M. Coxeter, Regular Polytopes, 1963, (Dover reprint, 1973).
[5] Walther Dyck, Katalog mathematischer und mathematisch-physikalischer Modelle, Apparate und Instrumente, 1892
[6] Gerd (Gerhard) Fischer, Mathematische Modelle, (Plates)and Mathematical Models: From the Collections of Universities and Museums (English Commentary), Vieweg, Braunschweig, 1986.
[7] Cyril H.H. Franklin, "Hypersolid Concepts, and the Completeness of Things and Phenomena," Mathematical Gazette, 21, Dec. 1937, pp. 360-364.
[8] Bathsheba Grossman, http://www.protoshape.com/
[9] George W. Hart, Geometric Sculpture, http://www.georgehart.com/
[10] G.W. Hart, "Icosahedral Constructions," in Proceedings of Bridges: Mathematical Connections in Art, Music and Science, Southwestern College, Winfield, Kansas, July 28-30, 1998, pp. 195-202.
[11] G.W. Hart, "Sculpture based on Propellorized Polyhedra," Proceedings of MOSAIC 2000, Seattle, August, 2000.
[12] G.W. Hart, "The Millennium Bookball," Proceedings of Bridges 2000: Mathematical Connections in Art, Music and Science, Southwestern College, Winfield, Kansas, July 28-30, 2000.
[13] G. Hart, "Solid-Segment Sculptures," to appear in Proceedings of Colloquium on Math and Arts, Maubeuge, France, 20-22 Sept. 2000, Springer Verlag.
[14] G. Hart, "Computational Geometry for Sculpture," Proceedings of ACM Symposium on Computational Geometry, Tufts University, June 3-5, 2001.
[15] G.W. Hart and Henri Picciotto, Zome Geometry: Hands-on Learning with Zome Models, Key Curriculum Press, 2001.
[16] John Jacob Holtzapffel, Hand or Simple Turning: Principles and Practice, 1881, (Dover Reprint, 1976).
[17] E.M. Horsburgh, Handbook of the Napier Tercentenary Celebration, 1914, (1982 reprint by Tomash Publ.)
[18] Peggy Kidwell, "American Mathematics Viewed Objectively: The Case of Geometric Models," in Vita Mathematica: Historical Research and Integration with Teaching, Ron Calinger ed., MAA, 1996, pp. 197-208.
[19] Mathcamp, http://www.mathcamp.org/
[20] Koji Miyazaki, An Adventure in Multidimensional Space: The Art and Geometry of Polygons, Polyhedra, and Polytopes, Wiley, 1983.
[21] William Mueller, Mathematical Wunderkammern, American Mathematical Monthly, to appear, 2001.
[22] Sanders, http://www.sanders-prototype.com/
[23] Martin Schilling, Catalog mathematischer Modelle fur den hoheren mathematischen Unterricht, Leipzig, 1911.
[24] Ludwig Schläfli, "Theorie der vielfachen Kontinuität," Auftrage der Denkschriften-Kommission der Schweizerischen naturforschenden Gesellschaft, 38, 1901, pp. 1-237. Partial English translation by Arthur Cayley, "On the Multiple Integral …," Quarterly Journal of Pure and Applied Mathematics, vol. 2 (1858) pp. 269-301, and vol. 3 (1860) pp. 54-68 and pp. 97-108.
[25] Victor Schlegel, "Theorie der homogen zusammengesetzten Raumgebilde," Nova Acta der Kaiserlichen Leopoldinisch-Carolinischen Deutschen Akademie der Naturforscher, 44(4), 1883, pp. 337-459 (plus plates).
[26] Victor Schlegel, Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren, 1986.
[27] John Skilling, "Uniform Compounds of Uniform Polyhedra," Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 79, pp. 447-457, 1976.
[28] D.M.Y. Sommerville, An Introduction to the Geometry of N Dimensions, 1929, (Dover reprint, 1958)
[29] D.M.Y. Sommerville, "Description of a projection-model of the 600-cell in space of four dimensions," Proceedings of the Royal Society of Edinburgh, 34, 1914, pp. 253-258 (plus plate).
[30] John Stillwell, "The Story of the 120-Cell," Notices of the AMS, Jan. 2001, pp. 17-25.
[31] Alicia Boole Stott, "Geometrical deduction of semiregular from regular polytopes and space fillings," Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam, (eerste sectie), Vol. 11, No. 1, pp. 1-24 plus 3 plates, 1910.
[32] W. I. Stringham "Regular Figures in n-Dimensional Space" American Journal of Mathematics, Vol. 3 no. 1, March 1880, pp. 1-14.
[33] Russell Towle, Regular-Polytopes, Mathematica notebook, 2000, http://www.mathsource.com/cgi-bin/msitem?0210-643.
[34] Z Corporation, http://www.zcorp.com/
[35] Zometool Corporation, http://www.zometool.com/
[36] 3D Systems, http://www.3dsystems.com/
I thank Dr. Peggy Kidwell of the Smithsonian Institution for research assistance and access to the Smithsonian's models in storage, Angela Vierling and John Sharp for providing valuable information and leads on the history of mathematical models, Imin Kao of SUNY Stony Brook for providing access to the machine on which Fig 16 was built, Carlo Sequin for funding the model of Figure 18, and Dr. Manfred Hofmann of RPC, Switzerland for the model illustrated in Figure 19.