The following is a webified version of: George W. Hart, "Icosahedral Constructions" Bridges: Mathematical Connections in Art, Music, and Science Reza Sarghani (editor),1998, pp. 195-202.

Icosahedral Constructions

George W. Hart

Abstract

A mathematical concept has inspired me to create a series of sculptures. While the media, surface forms, and general impact of these constructions may vary considerably, there is an ancient underlying structure common to the series. The mathematical basis behind these sculptures is the chiral icosahedral symmetry group. This underlying form binds these pieces in a way that may be obvious to a mathematician accustomed to the study of patterns, yet invisible to a casual observer. For centuries, geometry has been considered fundamental to an educated mind and has been both tool and inspiration to many artists, yet it has lost this status in our current culture. One purpose of my artwork is to show that geometry still has a power and a relevance. I hope to prod the viewer into seeing the type of deeper connection which is the subject of this series of sculptures. In addition, there is a natural aesthetic which many artists have found in polyhedral symmetry.

Icosahedral Symmetry

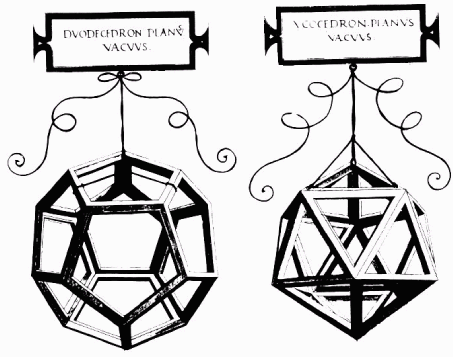
Fig. 1 Dodecahedron and icosahedron, by Leonardo Da Vinci for Luca Pacioli’s The Divine Proportion.

The ancient Greeks who wrote of the five Platonic solids certainly appreciated the geometric beauty which they embody. When any of us now turns a dodecahedron in our hand we see the same quintessential form which inspired Pythagoras and many others through the ages. Leonardo DaVinci’s drawings of the icosahedron and the dodecahedron, published in 1509, are shown as Fig 1. Although the dodecahedron may appear superficially very different from the icosahedron, there is a level of analysis at which they are identical.

We are all accustomed to geometric abstraction in which we think of ideal versions of physical objects. For example we may hold a handful of marbles and imagine an ideal Platonic sphere more perfect than any marble, free of even the atomic-scale imperfections present in any physical sphere. Similarly, we can imagine the ideal dodecahedron and the ideal icosahedron as distinct objects inhabiting a Platonic domain of polyhedra, free from the imperfections of any cardboard polyhedron model. Yet there is a deeper level — one floor down in Platonic structure — at which the ideal dodecahedron and ideal icosahedron are but two models of a single, more basic form which they share.

Fig. 2. The 31 symmetry axes of the icosahedron and dodecahedron, superimposed so they align (six 5-fold, ten 3-fold, fifteen 2-fold).

The deep structure common to the dodecahedron and icosahedron is termed their symmetry group. It is the pattern of rotations and reflections inherent in their geometric form. For example, a line passing through the centers of two opposite faces of a dodecahedron is a 5-fold axis of the dodecahedron. Rotating the dodecahedron about this axis through an angle of 72 degrees (or any multiple of 72 degrees) leaves it appearing unchanged. Altogether, there are six such axes for a dodecahedron (one axis for each pair of opposite faces), arranged at very specific angles to each other in space. The icosahedron, though made of triangles instead of pentagons, also has six 5-fold axes of symmetry arranged at the same angles. In the icosahedron, the 5-fold axes pass through pairs of opposite vertices. Similarly, both solids have ten 3-fold axes. They pass through opposite vertices of the dodecahedron and through the centers of opposite faces of the icosahedron. They also each have fifteen 2-fold axes which pass through the opposite edge-midpoints in either case. The total arrangement of symmetry axes is identical in the two cases as Fig. 2 illustrates. If one starts with a dodecahedron or icosahedron, constructs all of its symmetry axes, and then erases the polyhedron, one can not tell whether it was the dodecahedron or icosahedron that one started with.

Fig. 3 The 15 icosahedral symmetry planes, each represented by a disk.

The symmetry group common to the icosahedron and dodecahedron is usually called icosahedral, though it lies behind other polyhedra as well. It is different from the symmetry of many other polyhedra; for example, the cube has three 4-fold axes, four 3-fold axes, and six 2-fold axes. The sculptures shown below all have icosahedral symmetry. To fully understand them, one must see through not only the irregularities of technique which any physical object must manifest, but deeper—past their form—to the common symmetry group which binds them.

There is another aspect of polyhedral symmetry beyond axes of rotation. One can also look at the mirror planes of a polyhedron. The planes of symmetry are the imaginary planes passing through the center of the object which reflect one side to exactly match the other side. Again, the dodecahedron and icosahedron exactly agree in their symmetry planes. Each has fifteen planes of symmetry in exactly the same arrangement. Fig. 3 shows this arrangement, with one circle for each symmetry plane. The planes divide the surface of a sphere into 120 right triangles called Mobius triangles, which are alternately left-handed and right-handed. The symmetry axes are located where the planes intersect.

When one studies the possible sets of symmetries, what mathematicians call group theory, it turns out that only a relatively small number of polyhedral symmetry structures are possible. In the case of icosahedral symmetry, there are two possibilities: an object either has fifteen mirror planes or it has none. An object with no mirror planes is called chiral (Latin for hand). A chiral object appears different in a mirror; it comes in left-hand and right-hand forms. The opposite, e.g., the icosahedron which has one or more planes of reflection, is called reflexible.

Examples

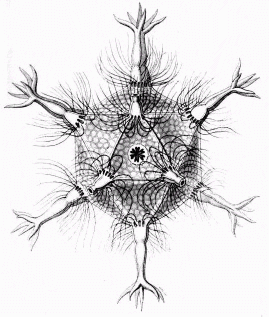
Fig. 4 Radiolarian, by Haeckel.

In nature, icosahedral symmetry does not show up at human scales, only at microscopic scales. The icosahedral symmetry of certain species of radiolaria are well known from the drawings of Ernst Haeckel. I surmise that he found this symmetry particularly attractive since he chose an icosahedral form for the first figure of the first plate of his beautiful 1904 collection, Artforms in Nature. It is shown here as Fig. 4. Other natural examples, all discovered relatively recently, include the forms of certain viruses, microscopic quasicrystals, and "fullerene" molecules. (Incidentally, crystals of iron pyrite do form as dodecahedra with equal 5-sided faces, but the faces are not regular pentagons, and so the crystals do not have any 5-fold axes of symmetry; they are not of the icosahedral symmetry group.)

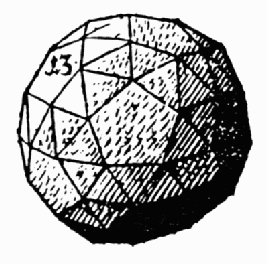
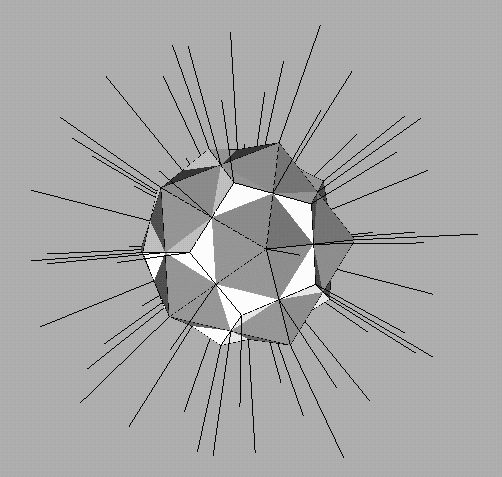
Fig. 5 Snub icosidodecahedron, discovered by Archimedes, rediscovered by Kepler.

Although the ancients discovered and created objects with icosahedral symmetry, I know of no surviving description of any chiral icosahedral object from that period. It is likely that Archimedes discovered the snub icosidodecahedron, and that this was the first example of chiral icosahedral symmetry known to humankind, but his writing on this topic is lost and only inferred from later commentaries. Kepler independently rediscovered Archimedes' lost snub icosidodecahedron, and published it in his 1625 book Harmonies of the World; see Fig. 5. One pentagon and four triangles meet at each vertex.

However, before Kepler, there was an independent discovery of this symmetry. The earliest surviving example I know of an object with chiral icosahedral symmetry is a 1568 drawing by Jamnitzer. His Perspectiva Corporum Regularium contains many beautiful imagined objects with icosahedral symmetry, e.g., his monument shown as Fig 6. However, only one, shown here as Fig 7, has chiral icosahedral symmetry. To come up on his own with something of this class is an enormous artistic and intellectual achievement in my view.


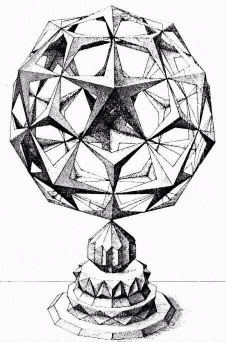
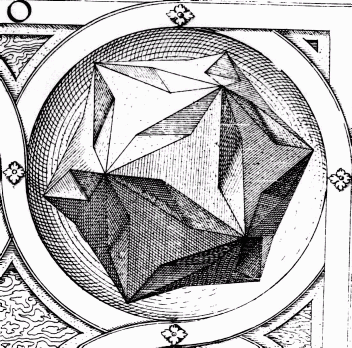
Fig. 6 An icosahedral monument by Wentzel Jamnitzer.	Fig. 7 Detail of a drawing by Jamnitzer.

These developments were part of a surge of interest in geometry and polyhedra in Renaissance Europe. Polyhedra were valued not just for their classical associations, but were considered worthy objects of an artist's study and important tests of an artist's mastery of the newly developed techniques of perspective. In Albrecht Durer's 1525 Painter's Manual, he not only teaches techniques of perspective, but he is the first to show polyhedra in print as an unfolded net. His net of the icosahedron is shown as Fig 8.

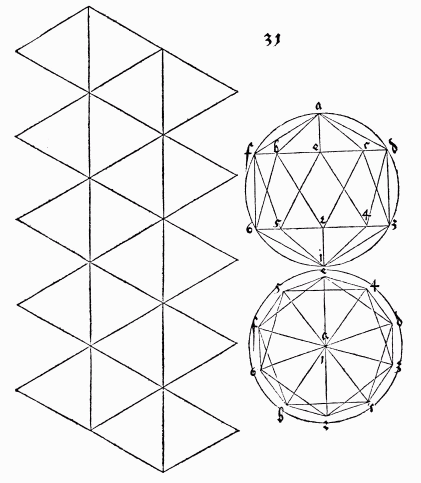
Fig. 8 The eariest known net of an icosahedron, by Albrecht Durer.

Although icosahedral forms have been created through the centuries since then, we now skip ahead to our century's most notable artist of polyhedra. M.C. Escher is best known for his tessellations, but he also had a great affinity to polyhedra. A chiral icosahedral object is featured in his lithograph Gravity, which shows a small stellated dodecahedron perforated in a chiral manner and then populated with colorful creatures. Even more relevant is that Escher made a number of sculptures with chiral icosahedral symmetry, including a puzzle of twelve intertwined starfish, and an icosahedral candy tin design. Fig. 9 shows Escher’s carved maple flower, made in 1958.

Fig. 9 Carved maple sculpture in the form of twelve flowers arranged as a dodecahedron, by M.C. Escher.

Method

A simple general method for seeing a construction with icosahedral symmetry is available, if the object is to be reflexible. The icosahedral kaleidoscope, invented by Mobius in 1852, is a set of three mirrors, each a thin circular wedge, with angles of 20.91, 31.72, and 37.37 degrees, respectively. They are arranged in the form one of the small triangles shown in Fig. 3, i.e., the points of the wedges meet at the center of the sphere, with the reflective side facing into the triangular region. If any object is placed in the triangle and viewed from inside the triangle, the "hall of mirrors effect" causes it to be replicated with the symmetry of an icosahedron. Details can be found in Coxeter [1963], but this method is not suitable when one is interested in chiral objects, which have no planes of symmetry.

To physically construct an object with chiral icosahedral symmetry, one first imagines the symmetry axes, then places components about them in the proper positions. For example, if one starts with sixty identical copies of anything, they can be placed on the surface of a sphere, five around each of the twelve points where the six 5-fold axes penetrate the sphere. However, if one starts with objects that have 5-fold symmetry, then only twelve are needed, as each can be centered over an axis. Similarly, twenty components with 3-fold symmetry can be placed at the 3-fold points, or thirty components with 2-fold symmetry can be placed on the 2-fold points.

One could analogously assemble 120 copies of a component (60 left-hand pieces and 60 righthand pieces) to construct a reflexible icosahedral model, but that symmetry group was not the subject of this series.

Constructions

In these constructions, the components are carefully designed both for the overall form which the assemblage is to achieve and for the necessary lengths and angles required to make the components meet properly. In some cases I have selected mass-produced elements to use as components, but in most cases I fabricate the elements to be assembled. However, the most challenging part of the construction of the following sculptures is the construction of the necessary jigs to hold the components together at the proper relative positions for assembly. I usually spend far more time constructing jigs than actually using the completed jigs to assemble components.

The sculptures shown here as Figs. 10-18 were all constructed by the author in 1997, as part of a series. Each displays the identical chiral icosahedral symmetry, but with very different forms and media. I leave it to the reader to locate the thirty-one symmetry axes in each case, and to decide if the symmetry carries a natural aesthetic within each piece.

Fig. 10. I’d like to make one thing perfectly clear. (18”) This is a construction of 30 identical pieces of clear acrylic plastic (plexiglass). Each piece started as a plastic parallelegram with two polished edges, then was heated (baked in an oven at 300 F for 3 minutes) and bent into a form with 2-fold symmetry. Cooled in a jig which maintains two edges at the proper relative angle, each piece is centered on a 2-fold axis of symmetry, and exactly spans the 63.4 degree angle between two 5-fold axes. These edges were beveled to a 72 degree angle, so five fit around an axis, and glued with a solvent cement.

Fig. 11. The Plastic Tableware of Damocles. (25”) This is a construction of 180 plastic dinner knives, in black, white, and grey. It can be seen as sixty equilateral triangles, each containing one knife of each color. The triangles are arranged in the form of a dodecahedron in which the pentagons are replaced by concave dimples of five equilateral triangles. Knives of a color can be seen to spiral around the axes of symmetry.

Fig. 12. Battered Moonlight. (21”) This is an icosahedral topological surface with one side and six edges, inspired by the work of Brent Collins. It is constructed of paper machee over a steel (hardware cloth) framework, and painted in white latex/acrylic. The twelve holes contain the 5-fold symmetry axes, and the six edges are each 5-fold symmetric “equators” about one 5-fold axis.

Fig. 13. Gazmogenesis. (12”) This is a construction of 30 identical pieces of copper. Each piece was cut into the shape of an elongated ellipse, hand formed into a curve with 2-fold symmetry, and the assemblage was soft soldered. The intention was to create a form both organic and geometric, reminiscent of a radiolarian with a spiked spherical body containing internal structure. Each copper ellipse spans one edge of an icosahedron, along a detoured route which passes through the interior.

Fig. 14. Fire and Ice. (24”) Sixty identical pieces of oak and ten strips of brass are interwoven. The wooden components were cut on a computer-controlled router table, then hand beveled to the proper dihedral angles. After the wood was glued, the brass strips were woven through the wood and each other, and soldered into loops. Each brass loop has 3-fold symmetry and circles a 3-fold axis of the whole.

Fig. 15. No Picnic. This is 16’ mobile with three major spherical assemblages of plastic tableware: one ball consists of 150 knives in three colors, one of 180 spoons in six colors, and one of 240 forks in six colors. The plastic utensils were jigged on frameworks built from a commercial plastic construction toy, glued with solvent cement, and then the jigs were disassembled and removed through the spaces between the utensils. The supporting booms are steel tubes.


Fig. 16. Fork component of Fig. 15 (23”).	Fig. 17. Knife component of Fig. 15 (29”).

Fig. 18. Spoon component of Fig. 15 (32”).

References

H.S.M. Coxeter, Regular Polytopes, Macmillan, 1963, (Dover reprint, 1973).
Peter R. Cromwell, Polyhedra, Cambridge, 1997.
Michele Emmer (editor), The Visual Mind: Art and Mathematics, MIT, 1993.
George W. Hart, Virtual Polyhedra, http://www.georgehart.com/virtual-polyhedra/vp.html
George W. Hart, Geometric Sculpture, http://www.georgehart.com/sculpture/sculpture.html
Jay Kappraff, Connections: The Geometric Bridge Between Art and Science, McGraw Hill, 1990.
Doris Schattschneider, M.C. Escher: Visions of Symmetry, Freeman, 1990.
Marjorie Senechal, George Fleck (eds.), Shaping Space: A Polyhedral Approach, Birkhauser/MAA, 1988.
Hermann Weyl, Symmetry, Princeton U. Pr., 1952.