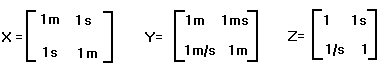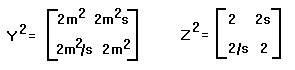Multidimensional Analysis
By Prof. George W. Hart
This web page gives a brief introduction to Multidimensional
Analysis,
a generalization of linear algebra which incorporates ideas from
dimensional
analysis. My book gives the full presentation, with
examples,
historical
discussion, and answered exercises, all at a level which assumes a
standard
undergraduate familiarity with linear algebra. You
can
purchase this book quickly and easily through Amazon.com.
"thoroughly recommended to those who really wish to
understand the theory of dimensions" -- Math
Reviews
The central idea is that vectors and matrices as used in science
and
engineering can be thought of as having elements which are not
just
real
(or complex) numbers, but formally have different types, such as length
or voltage. Quantities with different types do not form an
algebraic
field as they are not closed under addition, e.g., 1 meter + 1
volt
is undefined. Traditional linear algebra assumes that vectors and
matrices
are isomorphic to arrays of elements which are closed under
addition,
and
so traditional linear algebra is not formally valid for many
applications
in science and engineering.
Typically, scientists and engineers "drop" the units from
dimensioned
quantities and place just their numeric values as elements in
vectors
and
matrices. Doing so allows one to use traditional mathematical and
computational
tools on the resulting numeric arrays. Unfortunately, this is
misleading
as it causes one to miss the real mathematical properties of
vectors
and
matrices which contain dimensioned elements. Dimensioned matrices
have
very different properties from dimensionless ones. By examining
the
examples
below, one can see that traditional linear algebra can not be
isomorphic
to the algebra which scientists and engineers really need to use.
A. Scalars
One must begin with the study of ``dimensioned scalars," such as
1 volt,
and 2 meters. The study of their possible interrelationships
forms
an interesting branch of applied mathematics (or physics or
engineering)
called dimensional analysis. Traditionally this field only
concerns
scalar quantities (not vectors and matrices). You are probably
familiar
with it. The essential difference between dimensioned quantities and
traditional
algebraic structures is that it is not closed under addition, e.g.,
1
volt
+ 2 meters is undefined, yet they are part of the same algebra
as their product is defined.

A very useful computer program (which I have written and placed
in
the
public domain) for manipulating, converting, and calculating with
dimensioned
scalars is available. The program,
DimCalc, runs on PCs with Microsoft
Windows (3.1, 95, 98, or higher) software. The file to get is DimCalc.zip
which is a compressed package of the software and extensive
on-line
help
information. It includes the standard vbrun300.dll
subroutine
file in case you do not have it on your system already.
B. Vectors and Matrices
The linear algebra which results when one considers vectors and
matrices
which contain dimensioned quantities as their components is
surprisingly
interesting and rich. It is not an algebra over a field because the
elements
are not closed under addition. Although this algebra is implicit in
all
branches of modern engineering, it has not been carefully studied
before.
As motivation, consider these 2-by-2 arrays:
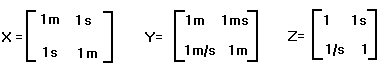
where m abbreviates meters, and s seconds. Try now to directly
multiply
out the matrix product X^2 using the standard formalism,
and
you
will see that the product X^2 is undefined, as its
diagonal
elements
would have to be the undefined sums "1m^2 + 1s^2". Thus the
familiar
property
that "any square matrix can be squared" does not hold in this
algebra,
as matrix products contain scalar sums, and sums are only
sometimes
defined.
If matrix elements are chosen carefully however, products are
defined.
The standard method of matrix multiplication shows that:
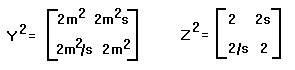
An important difference between Y and Z is that Z^2
preserves
the
dimensions of Z, so that Y^2+Y is
undefined,
while Z^2+Z is defined. As a consequence of this
property,
all integer powers of Z have the same dimensional
structure as Z.
In
particular, the Taylor series for the matrix exponential (or any
other
transcendental function) requires summing these powers, so exp(Z)
is
defined, but exp(X) and exp(Y) are undefined. These
different
properties show that X, Y, and Z come from
three different
classes of dimensioned matrices.
C. Pop Quiz!
If you think that you know linear algebra and that there is nothing
new
and interesting about matrices with scientific and engineering
quantities
like 1 meter, then take this simple quiz, and you'll find
out a
few things:
-
Note that X above has no determinant, while Y
and Z
do have a determinant: the product of the off-diagonal elements
of X
can not be subtracted from the product of the diagonal elements
of X,
as
would be necessary in the calculation of a 2-by-2 determinant.
One
might
now hypothesize a conjecture along the lines that "a square
dimensioned
matrix has a determinant iff it can be squared." That conjecture
is too
strong however. The "if" part holds but not the "only if." Find
a
2-by-2
counterexample, i.e., a matrix with a determinant but which can
not be
squared.
-
Find a square 2-by-2 matrix P such that P times
P
inverse
gives a different result from P inverse times P.
Of
course,
in traditional linear algebra, the product of a matrix and its
inverse
is the same regardless of order, (assuming an inverse exists,)
but
you're
not in Kansas anymore.
When you have solved these, check your answer
D. Some Surprising Theorems
Here a few interesting differences between traditional linear
algebra
and
dimensioned linear algebra:
-
On arbitrary n-by-n arrays of dimensioned quantities, most
familiar
algebraic
operations (e.g., products, determinants, eigenvalues, and the
singular-value
decomposition) are not defined. There are certain very special
classes
of dimensional structures for which these operations make sense,
and
only
these special forms are ever applied in engineering
applications.
-
The traditional concept of a vector as a quantity with direction
and
magnitude
is far too narrow for engineering purposes, while the
traditional
concept
of a matrix as an array of scalars is far too broad. (Most
vectors have
no magnitude. Most arrays are not matrices.)
-
The well-known restriction that the argument to transcendental
functions
in physical laws be dimensionless is only true for scalars. It
is not
true
in the multivariable case. For example, the matrix exponential,
for a
certain
class of dimensioned square matrices, including Z above,
is not
only well-defined, but essential to a proper treatment of linear
systems
analysis.
-
There is a natural nesting to many of the dimensional forms for
matrices.
For example, among the square matrices, the dimensionless
matrices of
traditional
linear algebra are a proper subset of the set of matrices that
can be
the
argument to the exponential, which is a proper subset of the set
of
matrices
that have eigenstructure, which is a proper subset of the set of
matrices
that have determinants and inverses, which is a proper subset of
the
set
of matrices which can be multiplied with other matrices, which
is a
proper
subset of the set of arrays in which the elements carry physical
dimensions.
-
Many well-known theorems do not hold for dimensioned matrices,
e.g.,
the null space of a matrix is the orthogonal
complement
of
the image space of its transpose
and
a matrix is positive definite if and only if its
eigenvalues
are positive.
In fact, the set of matrices for which definiteness is defined
barely
intersects
the set of matrices for which eigenvalues are defined. By
analyzing the
dimensional structures of these classes of matrices, flaws in the
traditional
proofs become obvious, along with the special conditions under
which
the
theorems hold.
- For a nonsingular square matrix, A with inverse B,
it is
true as expected that AB=I and BA=I, but in
general AB
does not equal BA. The explanation lies in the fact that
there
are
many different dimensionally distinct identity matrices.
E. Further Information
To learn more about these and other matrix classes, and other
phenomena
concerning dimensioned linear algebra and dimensional analysis of
matrix
relationships, be sure to check out my book, written for anyone with
an
undergraduate background in linear algebra. You
can
purchase this book quickly and easily through Amazon.com.
George W. Hart, Multidimensional Analysis: Algebras and
Systems
for
Science and Engineering, Springer
Verlag, 1995. ISBN 0-387-94417-6
Math major types might want to try this pithy summary paper, (available in postscript format) but it
is not for general audiences:
G. Hart, ``The Theory of Dimensioned Matrices,'' Proceedings of
5th
SIAM Conference on Applied Linear Algebra, Snowbird, Utah, June
1994,
pp.
186-190.