The (10, 3)-a Network
George W. Hart
Above is a sculptural concept based on
the crystal structure (10,3)-a,
described
in the 1950's by the chemist A.F. Wells. I have taken that
arrangement of vertices and edges and wrapped a smooth organic volume
around it using a general-purpose algorithm described here. The result is a
"slimmed down" gyroid surface. Above is a 4-by-4-by-4
block of the lattice structure made as a 3.5 inch nylon model using
selective laser sintering. Check out the various views below, but it is
impossible to convey its 3D structure with 2D
images. It would be better to look at the stl
file in a 3D
viewer or use it to make your own physical copy.



Looking down a 3-fold axis you see a hexagonal pattern of tunnels.

In any 110 direction, you get this pattern.

In other directions, you get other patterns. It is a very rich object!

The above rendering only hints
at how cool the real physical model is when you hold it.
For one thing, my version stands up on one corner, balanced nicely on the three feet in the lower-left.
For one thing, my version stands up on one corner, balanced nicely on the three feet in the lower-left.

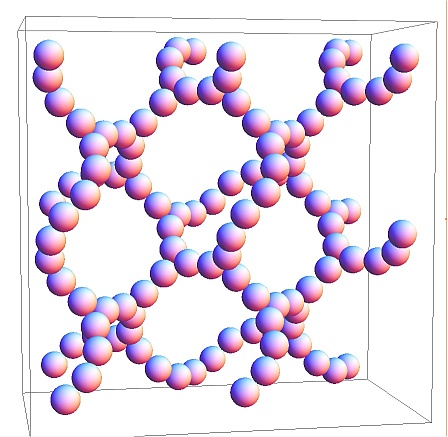
Looking down the X, Y, or Z axis
drections, you see the above pattern of large and small tunnels.

The above rendering gives more perspective.

The above rendering gives more perspective.

Looking down a 3-fold axis you see a hexagonal pattern of tunnels.

In any 110 direction, you get this pattern.

In other directions, you get other patterns. It is a very rich object!

Wells points out that the structure
can
interpenetrate space with its mirror image.
This colored rendering clarifies that there are two separate components.

A physical model of the two interlocked structures is immensely complex.
The two parts in the above 3.5 inch nylon model are free to jiggle slightly.

Here is the view of the doubled structure along an X, Y, or Z direction.
This one is a 5-by-5-by-5 block of doubly covered unit cells.
(This doubled model also stands up nicely, balanced on a corner!)

This colored rendering clarifies that there are two separate components.

A physical model of the two interlocked structures is immensely complex.
The two parts in the above 3.5 inch nylon model are free to jiggle slightly.

Here is the view of the doubled structure along an X, Y, or Z direction.
This one is a 5-by-5-by-5 block of doubly covered unit cells.
(This doubled model also stands up nicely, balanced on a corner!)