As far as I know, this is the only two-layer geodesic sphere anyone has ever made that is chiral, meaning not the same as its mirror image.  The outer layer consists of 260 triangles. The inner layer has 12 pentagons and 120 hexagons. It is 4 inches in diameter and extremely rigid.



I made this from nylon using rapid prototyping techniques.  My software can make a wide range of structures and I chose this particular one to be of reasonable complexity for the fabrication process. This one is based on the (3,1) Goldberg polyhedron. What that means is illustrated above. To go from one 5-fold hub to another, you go three steps out, then turn right and go one more step. In the mirror-image version, you would turn left. These (a,b)-frequency geodesic spheres, where b is non-zero and not equal to a are called "Type 3" geodesic spheres. Because they are chiral, a larger inventory of lengths and angles is required to make them.  So this type of design is not as cost effective for large physical domes and I don't know that anyone ever made one before.  However, I find them the most visually interesting for sculptural purposes.



It is a fairly complex structure. The above rendering fogs out the back, which makes it easier to see just the front.


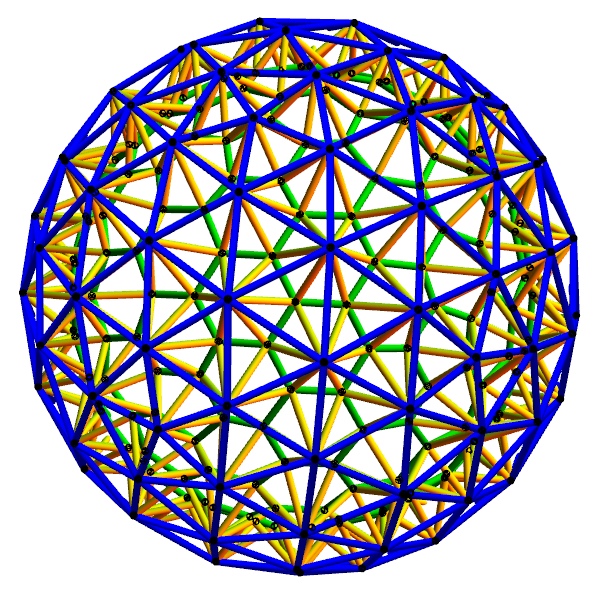
Or perhaps this color-coded rendering of just the front is clearer.  The outer layer of triangles is blue, the inner layer of hexagons and pentagons is green, and the connecting layer of struts is yellow.

The STL file which you can use to make a copy of it is available on my Rapid Prototyping page.