Polyhedral Clusters

With a good 3D printer, it is possible to make some beautiful polyhedral assemblages. Above is a second-order fractal construction, composed of 144 small stellated dodecahedra, in twelve groups of twelve structured like an icosahedron of icosahedra. It is about 11 cm long, made of nylon by selective laser sintering. The stl file to make your own copy or to view it in 3D is here.

Its appearance can vary greatly depending on your viewpoint. Above is the same object (without my hand this time) viewed along a 5-fold axis.

And here it is again, but now looking along a 3-fold axis, so you can see a bit of the interior. But only by holding it in your hand and spinning it around can you get a full sense of how cool it is.

Here is a separate model of just twelve small stellated dodecahedra. Each touches its five neighbors at the tips of five of its arms. The units are centered on twelve points, arranged like the vertices of an icosahedron. Ideally---to a mathematician at least---each would contact its neighbors at just a single point, but for engineering strength, I designed enough overlap of the tips that it doesn't fall apart. Twelve of these groups combine to make the larger structure at the top of the page.

And, just to be clear about what a single small stellated dodecahedron is, here is the oldest known presentation of one. This is a photo I took of the mosaic floor in the Basilica of St. Mark, Venice. This mosaic is usually attributed to Paolo Uccello (1397-1475). Artists have been inspired by this polyhedron for hundreds of years . Some impressive clusters of small stellated dodecahedra can be seen in the sculpture of Morton C. Bradley.

In principle, one can create higher-level clusters, but the complexity grows exponentially with the level, so the tiny components are likely to fall apart when fabricated. Above is a rendering of the third-level cluster in this family, consisting of twelve of the second-level units. I haven't tried to fabricate any third-level constructions. In fact, I haven't tried any other second-level clusters than the one illustrated at the top of the page.

Variations

The general idea is to choose any polyhedron as a "seed" and make clusters by replicating it at the vertices of an imagined larger polyhedron, then make clusters of clusters similarly. In the above examples the seed is the small stellated dodecahedron, the clustering arrangement is the vertices of an icosahedron, and only the level is varied. But I have fabricated a variety of first-level clusters with other parameters, to see how they look and how well they hold together. I plan to take some of these to the second level in the future. Below are some of the models I have made. Each is about three inches in diameter, made of nylon by selective laser sintering.

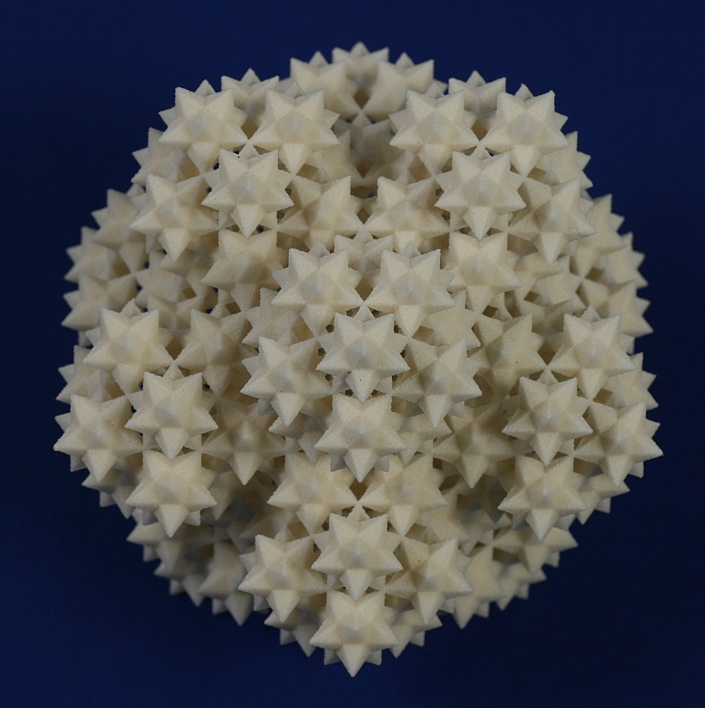
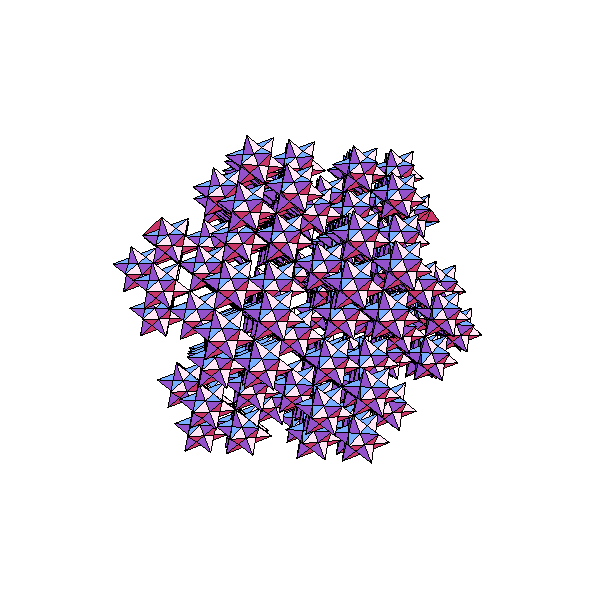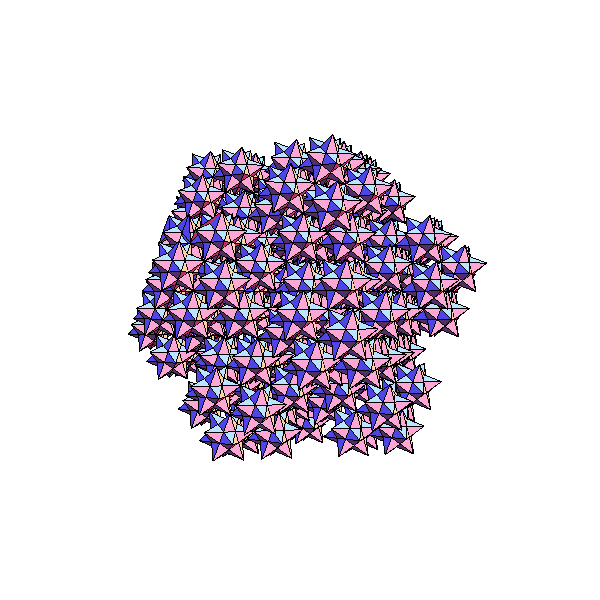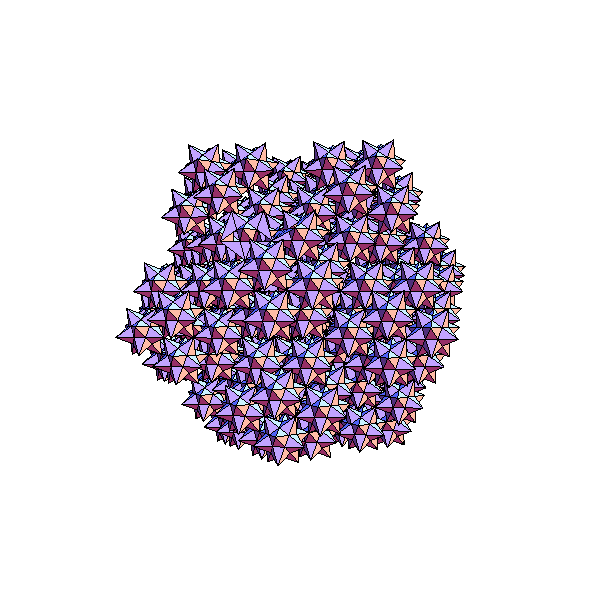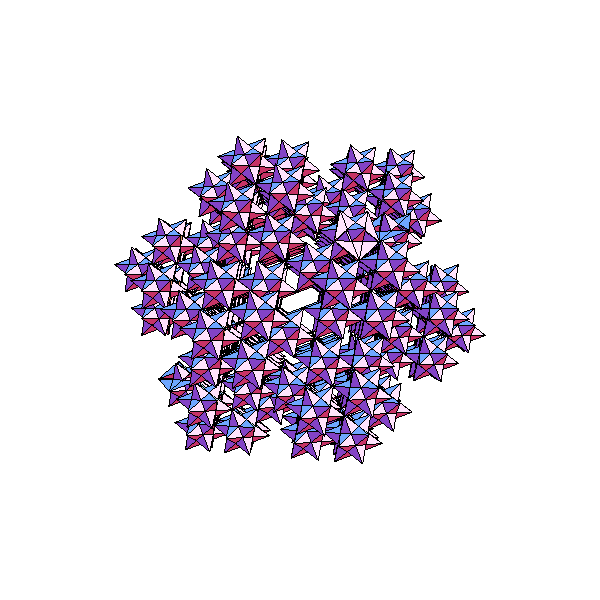Twenty great icosahedra arranged as the vertices of an icosahedron.

Same as above, looking down a 3-fold axis.

The same again, looking down a 5-fold axis, to emphasize it's floral feeling.

Thirty small stellated dodecahedra, at the vertices of an icosidodecahedron.

Same as above, looking down a 3-fold axis.

Here is a 3-fold view of a different cluster of 30 small stellated dodecahedra at the vertices
of an icosidodecahedron. Here, each has been rotated 90 degrees compared to the above.

Twenty great dodecahedra, looking along a 3-fold axis.

Thirty great dodecahedra, arranged as the vertices of an icosidodecahedron.

Twenty great icosahedra, arranged as the vertices of a dodecahedron.

Same as above, looking at a 3-fold axis.

A simple program can generate many beautiful fractal forms of this type. The program I used is described in Section 8 of this paper:

G. Hart, "Procedural Generation of Sculptural Forms," in Proceedings of Bridges 2008, pp. 209-218.

The paper is available here and you can download the Mathematica program as well. Then with access to a 3D printer, you can start making your own beautiful polyhedral clusters.

And to conclude, here is another view of the cluster shown at the top of this page.