Skewer Hyperboloids

George W. Hart



I was invited to do a workshop for a math enrichment class at Brookhaven National Laboratories, and decided to try having everyone construct hyperboloids from skewers.  As you can see, it worked out quite well.  Here are instructions for you to make your own.



This is a hyperboloid (also called a "hyperboloid of one sheet").  It is a smooth continuous surface that can be obtained by rotating a hyperbola around an axis.  (Actually, this is just part of an infinite hyperboloid surface; the top and bottom circles are where I arbitrarily cut it off; a complete hyperboloid has no edges.)  Surprisingly, it is a ruled surface, which means every point in it lies on a straight line that is embedded in the surface.


Here we can see red line segments going in one direction and blue ones going in the other direction. We will use skewers to indicate these lines.  Unlike mathematical lines, skewers can not intersect each other, so plan to have the red ones slightly outside of the blue ones.  To hold everything together, we will use small rubber bands at the crossings. I found these rubber bands work well, but other small, inexpensive rubber bands might work just as well.  I found that heavy twelve-inch skewers work quite nicely, but ten-inch skewers are too flexible. The only other material required is a sheet of heavy paper (card stock) and a bit of tape.




Start by deciding how many skewers you will use in each direction and call that number n.  I recommend using n equal to something in the range of twelve to sixteen, up to twenty at the very most and only if you are ambitious.  Cut two long strips of heavy paper and tape them together to make a double-long strip.  Poke n holes in the strip, at roughly one-inch spacing, as shown above.  This paper strip will serve as a temporary scaffold, and will be removed later.




Now make n pairs of skewers.  Each pair is X-shaped, joined in the middle with a rubber band.  With the rubber bands we used, we had to wrap it around two or three times to make a tight connection. Poke one of a pair into a hole, for each of the n holes.




It will be tricky at first to keep them organized and prevent everything from getting into a tangle.  The vertical approach above didn't work.  Keeping the strip flat on the table did.




Did I mention not to poke your finger on the sharp points?




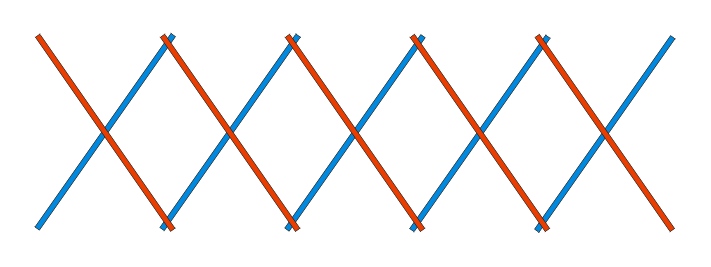
Now think of the red and blue pattern above, but keep it flat, not "cylindrical," for the moment.  Systematically tilt all the skewers that go through the paper one way (the red family) and tilt the others (the blue family) the other way. Be sure the red ones are always on top of (or always below) the blue ones.  (Which way you tilt each family and which family is on top doesn't matter, as long as you pick a pattern and stick with it.) 



Add rubber bands along the tops where each skewer crosses its neighbor.  Also add rubber bands along the bottoms where each crosses its neighbor from the other side.  Make three nice, straight rows of rubber bands.



After three rows of rubber bands, slide the end rubber bands closer to the center row, to make a larger tilt angle, which adds more crossings. Add a fourth row of rubber bands that holds this next crossing.  At this point the paper can be ripped away and you will have a nice "accordion" band that opens and closes in an amusing way. Check all your reds are on top and all your blues are on the bottom. If you have an over-and-under weave like a basket, the skewers can not be in straight lines, so remove rubber bands as necessary, cross the skewers properly, and reconnect them so one family of skewers is always outside and the other family is always inside.




Wrap your band into a cylinder form, and rubber band the connections that go from one end to the other.  Again, be very careful that the "red" ones are always outside of the "blue" ones.




You should find that it springs open and closed nicely.




It will naturally spring into a circular cross-section.




As you keep adding rows of rubber bands, it will show more curvature.  Just push the existing rows slightly towards the middle to create more tilt and more crossings.  Keep them straight.  Add an additional row at the top or bottom, being careful about the over and the under.




I  found that it has a beautifully curved appearance when the number of rubber band rows is roughly two thirds of n.




This one has n=16 and 11 rows of rubber bands. So there are 32 skewers and 176 rubber bands.




This construction activity appeared in the Math Monday column on the Make Magazine blog from the Museum of Mathematics.



Thank you Cindy Lawrence for the workshop photos.