Fig. 1. Deep Structure, George W. Hart, 2000
Fig. 1. Deep Structure, George W. Hart, 2000
Figure 1 shows a 10 cm diameter sculpture titled Deep Structure, consisting of five nested concentric orbs. Each of the five has the same structure as the outer, most visible, orb: there are 30 large 12-sided oval openings, 12 smaller 10-sided openings, 80 irregular hexagonal openings, and 120 small rectangular openings. Oval "corkscrew spirals" in the 12-sided openings connect the layers with each other. The concept is based on familiar concentric ivory spheres which are traditionally turned on a lathe and hand carved, with holes in each layer providing access to the inner layers. However, Figure 1 is created in plaster by an automated 3D printing process, without any human hand. After I design such a sculpture as a computer file, it is fabricated in a machine which scinters, laminates, or solidfies thousands of very thin layers. [2] This piece and the next were printed by Zcorp [16].
Figure 2 shows a second 3D printing sculpture, about 8 cm in diameter. This is based on a projection of the regular 4-dimensional polytope called the "120-cell," but adapted into a more textured, chiseled form. There are many 5-sided openings and passages throughout its volume. The title Five-Legged-Bee Hive whimsically refers to the fact that bees with six legs make six-sided hives. (Thank you to Sandor Fekete for the suggestion.)

Fig. 2. Five-Legged-Bee Hive, George W. Hart, 2000
Both these sculptures can be idealized as a set of line segments connecting points in three-dimensional space. However, the lines here are not simple cylindrical rods. I designed angular, faceted struts to give these works more sculptural presence.
Leonardo da Vinci invented a solid segment representation of polyhedra for the illustrations to Luca Pacioli's 1509 book, De Divine Proportione. Prior to this, polyhedra were illustrated as either opaque solids or transparent line drawings. Opaque representations have the disadvantage of hiding the rear structure. Simple line drawings can produce the "Necker cube" illusion, in which it is not clear whether a line belongs to the front or rear surface. In Leonardo's new form of representation, thick segments and open faces show the front and back structure, avoiding both problems.
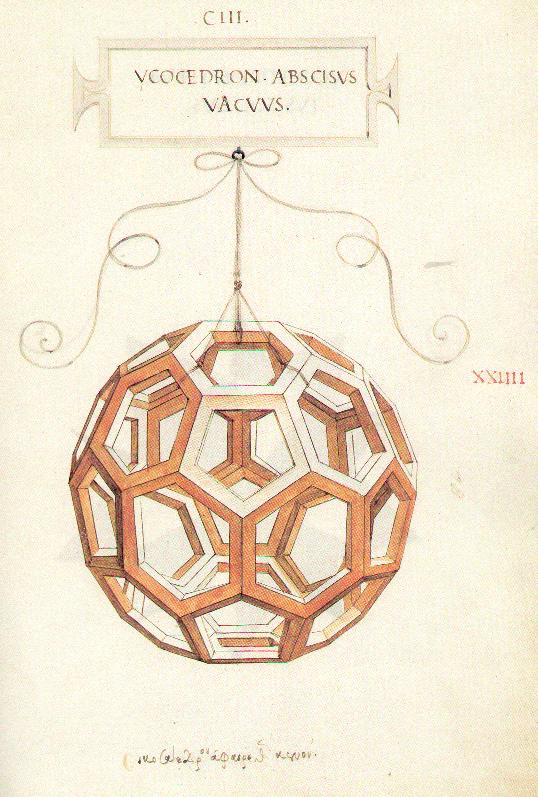
Figure 3. Leonardo "solid segment" presentation of truncated
icosahedron.
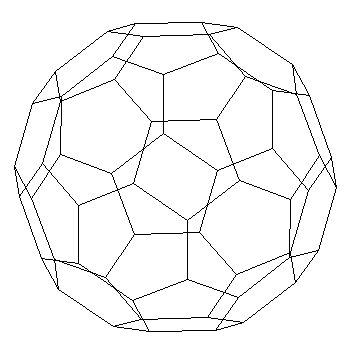
Figure 4. Line drawing of truncated icosahedron displays
"Necker cube" ambiguity between front and rear surface.
Many styles for solid-segment models are possible. Consider, for example,
molecular models used by chemists, with cylindrical struts and spheres
at each vertex. Leonardo used consistent, implicit rules in his 3D designs
such as Fig. 3: (1) outer faces of struts are made in the planes of the
polyhedron faces, (2) the inner faces are parallel to the outer faces,
and (3) the "side faces" are perpendicular to the inner and outer faces.
This makes for a very lucid presentation of convex polyhedra, but it does
not generalize to an arbitrary network of vertices and segments, in which
the structure need not determine planes tangent to the surface of a sphere.
In the design of geometric sculpture, I faced the problem of connecting
a set of points in space with faceted struts of some form, and needing
an algorithmic procedure to design interesting struts.
As background, consider two approaches to this problem that were found unsuitable. The Union operator of constructive solid geometry is a standard tool for combining 3D objects into more complex objects. [2] It is straightforward to produce prisms, antiprisms, or other approximations to cylinders for each segment and then call a Union subroutine to combine them. However, this approach fails in practice for large data sets, because of the instability of the union operator when using floating point data, even in large, expensive, commercial software packages. Plus, a serious drawback to this approach is that if it succeeds, it results in a large number of polygons.
Another approach is to create cylindrical approximations for each strut
as above, but not to union them as 3D objects. Instead the effect
of the union operation may be achieved on a voxel scale in the cross-sectioning
software which creates the layer data that control the 3D printing.
Again, there is a likelihood that the software will fail when given a complex
structure with many overlapping components. But more fundamentally,
these structures will not be visually lucid, because the orientation of
the faces of the cylindrical approximations are designed individually,
so are not relevant to the overall structure.
Step 3. Make Struts. Given two polygons that surround the ends of a line segment, take their convex hull to construct a "prismatoid" that surrounds the body of the segment. A prismatoid is the convex hull of two parallel polygons; its sides are triangles and/or quadrilaterals; special cases include the prism and the antiprism. Our "prismatoids" might not be formally prismatoids because the two bases may not be exactly parallel. This "prismatoid" step is done for every given segment after constructing appropriate polygons at each end.
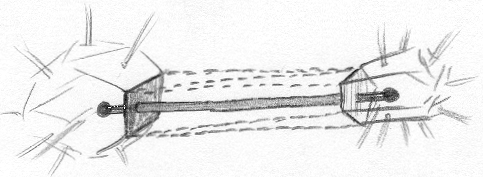
Figure 5. In Step 3, the convex hull of two polygons
(shaded) gives a "prismatoid" (dotted) around each segment.
Step 2. Make Polygons around Endpoints. In order to form these segment-surrounding polygons, we construct a simple convex polyhedron around each endpoint in such a way that its vertices lie between the outgoing segments. This is simply the dual to the convex hull of the points where the segments intersect a small sphere. For example, if six orthogonal segments meet at a given endpoint (Fig 6a) they define the six vertices of a small octahedron surrounding that point (Fig 6b). The dual to the octahedron is a cube (Fig. 6c) which has six square faces, one surrounding each segment.
Notice that this dual polyhedron can be scaled for thicker or thinner struts, within certain limits. This is called the scale factor parameter, and can be different for each vertex.
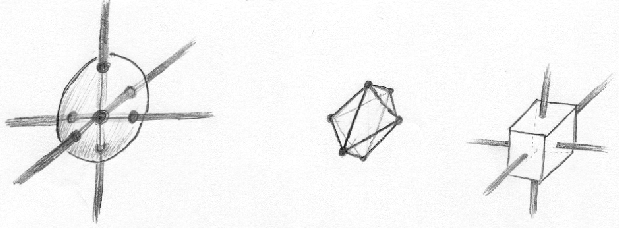
Figure 6. In Step 2, a) construct points around a vertex
where segments meet small sphere, (b) form their convex hull, and (c) construct
dual polyhedron.
Step 1. Ensure Endpoints are Enveloped. The step 2 procedure would fail if there were not enough points to define a polyhedron. So if there are fewer than four segments at a vertex, we first add "pseudo segments" to make a tetrahedral arrangement. Even with more than four, the arrangement may fail to form a polyhedron that surrounds the given engpoint, e.g., if the segments all lie in a plane or half-space. There is a short list of troublesome configurations to search for, illustrated in Fig. 7.

Figure 7. In Step 1, if the real segments (dark) do not produce
an arrangement which surrounds the vertex, add "pseudo segments" (light)
which do.
The following list of cases, in this sequence, seems to be sufficient: (other methods could be emplyed)
a) If there is only one segment, add three more as a regular tetrahedron.Cases (d) and (e) are not exclusive; consider a small fan of segments. The nature of duality guarantees that every face of the dual surrounds either a segment or a pseudo-segment. The faces which surround the real segments are used as the bases of the prismatoids. They are not output as part of the result. Only the sides of the prismatoids and the faces which surround pseudo-segments are output.
b) If there are two segments not opposed, add two more as a tetrahedron.
c) If there are two opposed segments, add three on their "equator" as a triangular dipyramid.
d) If all the segments lie in a plane, add two "poles" orthogonal to the plane.
e) If all the segments lie in a half-space, add one in the direction opposite their mean.
All the above operations are straightforwardly implemented with standard
vector operations. A suitable 3D convex hull subroutine is requred, but
this is a well-studied problem and many implementations exist.
5.1 Deep Structure. Shown in Figure 1 above, there are 720 struts in each of the five layers plus 480 struts which connect adjacent layers. The 4080 segments are wrapped with 27214 triangles altogether, which bound the struts.The close-up image in Figure 8 shows some of the diagonal inter-layer struts, and makes clear the slight degree of randomness introduced because they start at a random phase in each oval.
Figure 8. Closeup view of Figure 1 shows texture and layering.
For the structure of each layer, I chose the edges of a 31-zone zonohedron, illustrated in Figure 9, which has edges in the 31 directions of the icosahedron's axes of symmetry. It is a 242-sided polyhedron bounded by thirty 12-gons, twelve 10-gons, eighty 6-gons, and one hundred twenty squares. [11] It is particularly easy to build a physical model of this polyhedron with the Zometool modeling set. [14] Figure 9 is generated by a program I wrote which presents polyhedra in the solid-segment style of Leonardo da Vinci, discussed above, which helps to make clear the elegant structural aspects of this polyhedron. Although it is straightforward to make a 3D printing of the form in Figure 9, I would consider that a mathematical model, not a sculpture. Comparing it to Figures 1 and 8 should make clear the type of sculpted, chiseled look I was after.

Figure 9. 31-zone zonohedron that underlies each layer
of Figs 1 and 8.
5.2 Five-Legged-Bee Hive. Shown in Figure 2 above, this sculpture is based on the 120-cell. The underlying 4-dimensional structure consists of 120 regular dodecahedra, arranged so three meet around each edge and four meet at each vertex. In 3D, regular dodecahedra do not pack like this without gaps, but in 4D there is freedom to rotate them slightly to pack snugly. A shadow of the 4D edge arrangement onto 3D space gives the mathematical form underlying this sculpture. If the edges were straightforwardly rendered by the above algorithm, the structure in Figure 10 could result, but for 3D printing the struts would probably be made thicker. However, as a sculptor, I am interested in modifications which produce visually interesting effects, so I made a small variation to the algorithm, by which the faces corresponding to pseudo-struts are placed further from their vertex than other faces. This is actually accomplished by making the pseudo-strut points closer to the vertex before taking the dual in step 2 above. Doing so produces the sculptural form of Figure 2 rather than the mathematical model in Figure 10.

Figure 10. Edges of 120-cell orthogonally projected from 4D
to 3D, along the direction to the center of a cell
5.3 120-cell projected as "Schlegel Diagram" Figure 11 shows the design for a perspective projection of the 120-cell into 3D space, taken from very close up in 4D space. The effect is analogous to a 2D "Schlegel diagram" [3] of a 3D polyhedron. There are 119 dodecahedral cells packed inside the 120th outer cell. In general, elegant effects can result if the strut scale factor varies as a function (either increrasing or decreasing) of the distance of a vertex from the polytope center. In this case, the small inner cells are made with a strut thickness proportional to their smaller distance from the center. This design was worked out in discussions with Carlo Sequin. The 3D printing in Figure 12 is 5 cm across, executed and photographed by Bathsheba Grossman [4] with a Sanders prototype machine [17].
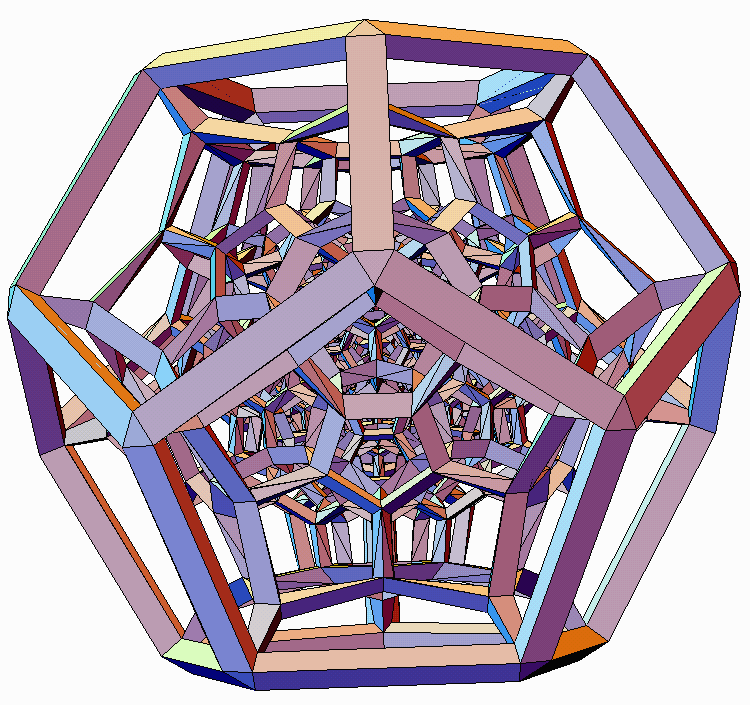
Figure 11. 120-Cell projected in perspective, like Schlegel
Diagram

Figure 12. Wax realization of Figure 11, 5 cm diameter
5.4 Truncated 120-cell. An as-yet-unrealized form is analogous to Figure 10, but truncated (in 4D) at each vertex. This is a cell-first orthogonal projection of the "truncated 120-cell," a 4D polytope consisting of 120 truncated dodecahedra and 600 regular tetrahedra, first described in a 1910 paper written by Alicia Boole Stott (a daughter of George Boole) [3, 15]. In this projection it produces a stunningly beautiful 3D form with 10-sided passageways piercing it in six different directions A large and very rewarding physical model can be made using Zometools; instructions are given in [14].

Figure 13. Projection of edges of truncated 120-cell
[2] Marshall Burns, Automated Fabrication: Improving Productivity in Manufacturing, Prentice Hall, 1993.
[3] H.S.M. Coxeter, Regular Polytopes, Dover reprint, 1963.
[4] Bathsheba Grossman, http://www.protoshape.com/
[5] G.W. Hart, Geometric Sculpture, http://www.georgehart.com/
[6] G.W. Hart, "Sculpture based on Propellorized Polyhedra," Proceedings of MOSAIC 2000, Seattle, August, 2000.
[7] G.W. Hart, "The Millennium Bookball," Proceedings of Bridges 2000: Mathematical Connections in Art, Music and Science, Southwestern College, Winfield, Kansas, July 28-30, 2000.
[8] G.W. Hart, "Reticulated Geodesic Constructions," Computers and Graphics, to appear 2000.
[9] G.W. Hart, "Loopy," to appear in Humanistic Mathematics.
[10] G.W. Hart, "Icosahedral Constructions," in Proceedings of Bridges: Mathematical Connections in Art, Music and Science, Southwestern College, Winfield, Kansas, July 28-30, 1998, pp. 195-202.
[11] G.W. Hart, "Zonohedrification," The Mathematica Journal, vol. 7 no. 3, 1999.
[12] G.W. Hart, "Zonish Polyhedra," Proceedings of Mathematics and Design '98, San Sebastian, Spain, June 1-4, 1998.
[13] G.W. Hart, "Calculating Canonical Polyhedra," Mathematica in Research and Education, Vol. 6 No. 3, Summer, 1997, pp. 5-10.
[14] G.W. Hart and Henri Picciotto, Zome Geometry: Hands-on Learning with Zome Models, Key Curriculum Press, 2001.
[15] Alicia Boole Stott, "Geometrical deduction of semiregular from regular polytopes and space fillings," Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam, (eerste sectie), Vol. 11, No. 1, pp. 1-24 plus 3 plates, 1910.
[16] Zcorp, http://www.zcorp.com/
[17] Sanders, http://www.sanders-prototype.com/
— DRAFT —