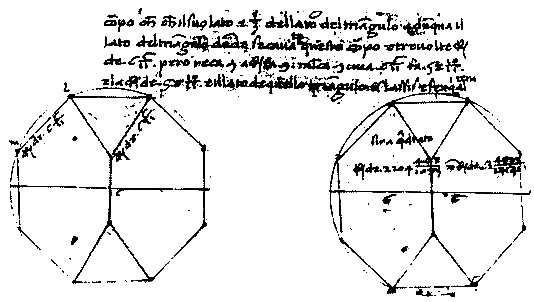
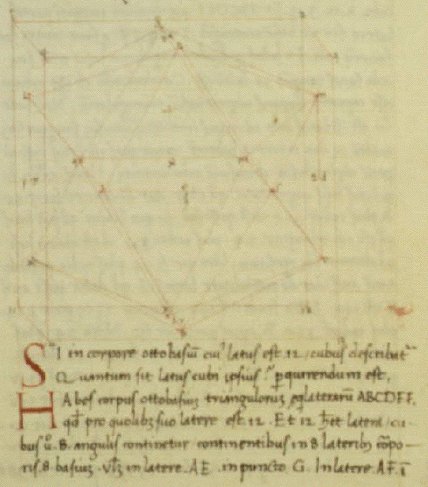
Piero is the first of a series of artists whose geometric explorations involved the gradual rediscovery of the Archimedean solids. He rediscovered the five Archimedean solids which are truncated Platonic solids: the truncated tetrahedron, truncated octahedron, truncated cube, truncated dodecahedron, and truncated icosahedron. These were presumably known to Archimedes, but that was not known in Piero's time. In addition, he rediscovered the cuboctahedron (mentioned by Plato). These six solids are employed in new and substantial geometric problems --- calculating the edge length of the solid given the radius of their circumsphere.
 The
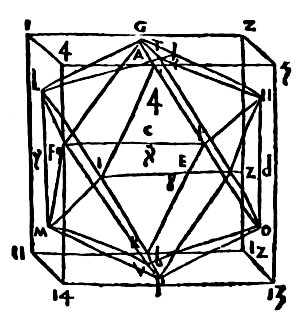
fact that each vertex of an icosahedron can be placed thusly in a face
plane of a cube is a beautiful Platonic
relationship discovered by Piero, the only one not described in Euclid's
Elements. As such it is a genuinely new piece of polyhedral
mathematics, and marks the beginning of the Renaissance fascination with
polyhedral geometry.
The
fact that each vertex of an icosahedron can be placed thusly in a face
plane of a cube is a beautiful Platonic
relationship discovered by Piero, the only one not described in Euclid's
Elements. As such it is a genuinely new piece of polyhedral
mathematics, and marks the beginning of the Renaissance fascination with
polyhedral geometry.
A clearer image, at left, comes from the printed version of Pacioli's
De Devina Proportione, which plagarized Piero's manuscripts, but
did have the positive effect of widely disseminating his discoveries.
 Exercise:
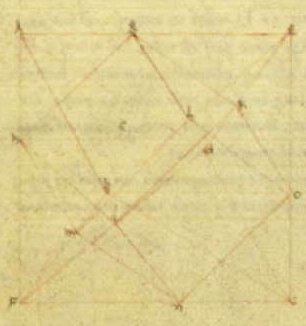
On the facing page of his Libellus, Piero shows another interesting
and original construction. I stared at this for quite a while before
figuring out what it is. I recommend you stare at the illustration
at right for a while to see if you can make it out. Hint: it involves
two Platonic solids.
Exercise:
On the facing page of his Libellus, Piero shows another interesting
and original construction. I stared at this for quite a while before
figuring out what it is. I recommend you stare at the illustration
at right for a while to see if you can make it out. Hint: it involves
two Platonic solids.
Answer: Piero is showing a nonstandard method of inscribing a cube in a regular octahedron. The eight vertices of the cube lie on eight of the twelve edges of the octahedron. It differs from the standard method of inscribing a cube in an octahedron in that they are rotated 45 degrees relative to one another, about one of the 4-fold axes. This is not a standard Platonic relationship because only one set of their three pairs of 4-fold symmetry axes are aligned.
I have no idea how Piero thought about this construction, but it is interesting to note some geometric and artistic consequences of it: There are three different ways to so inscribe a cube within the same octahedron. Superimposing the three (and then erasing the octahedron) gives a well-known compound, the compound of three cubes. Dualy, there are three different ways of so placing an octahedron around the same cube. Superimposing the three gives the compound of three octahedra. Interestingly, Escher employed both of those compounds.
For a recent study of Piero's life and times, see Marilyn A. Lavin (ed.), Piero della Francesca and his Legacy, 1995.