 The
Archimedean solid in which three squares and a triangle meet at each vertex
is the rhombicuboctahedron.
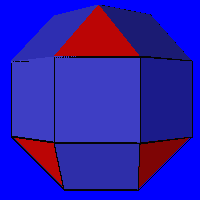
Related to it is another, similar, convex solid with three squares and
an equilateral triangle at each corner, called the pseudo-rhombicuboctahedron,
shown at right. Another name for it is the elongated square gyrobicupola,
and it appears as number 37 in Johnson's list
of convex polyhedra with regular faces.
The
Archimedean solid in which three squares and a triangle meet at each vertex
is the rhombicuboctahedron.
Related to it is another, similar, convex solid with three squares and
an equilateral triangle at each corner, called the pseudo-rhombicuboctahedron,
shown at right. Another name for it is the elongated square gyrobicupola,
and it appears as number 37 in Johnson's list
of convex polyhedra with regular faces.
The pseudo-rhombicuboctahedron is not classified as a semi-regular polyhedron, because the essence (and beauty) of the semi-regular polyhedra is not about local properties of each vertex, but the symmetry operations under which which the entire object appears unchanged. The pseudo-rhombicuboctahedron has only the dihedral symmetry of a square antiprism (one 4-fold axis, four 2-fold axes, and four mirror planes), not the full cubic symmetry of the rhombicuboctahedron (three 4-fold axes, four 3-fold axes, six 2-fold axes, and nine mirrors). Introductory texts which define the Archimedean polyhedra as having regular faces and identical vertices are misleading in this respect.
The pseudo-rhombicuboctahedron has been repeatedly re-discovered. For
example, the 1956 book Convex Figures and Polyhedra by L. A. Lyusternik
contains this interesting passage:
- It is remarkable that in the theory of semiregular polyhedra, which
is over 2000 years old, there was a defect, which was recently discovered
by the Soviet mathematician V. G. Ashkinuz. He discovered a 14th semiregular
polyhedron [figure of pseudo-rhombicuboctahedron] which differs
from the one shown in [figure of rhombicuboctahedron] only in that
the upper part, consisting of 5 squares and 4 equilateral triangles, is
rotated through an angle of pi/4. In the past these two semiregular polyhedra
were not distinguished.
But the earliest presentation I know of the pseudo-rhombicuboctahedron is in the form of its Schlegel diagram, illustrated in a 1905 paper by Duncan M. Y. Sommerville, "Semi-regular Networks of the Plane in Absolute Geometry," Transactions of the Royal Society of Edinburgh, Vol 41, Part III, no. 29, pp. 725-747, plus plates. (See Fig 27.)
 There
is an interesting non-convex polyhedron
analogous to the pseudo rhombicuboctahedron. First, familiarize yourself
with the great rhombicuboctahedron,
which is a non-convex relative to the rhombicuboctahedron. They both consist
of eight triangles and eighteen squares (six in the planes of a cube's
faces and 12 in the planes of a cube's edges), with three squares and one
triangle meeting at each of the 24 vertices. They have the same topological
structure.
There
is an interesting non-convex polyhedron
analogous to the pseudo rhombicuboctahedron. First, familiarize yourself
with the great rhombicuboctahedron,
which is a non-convex relative to the rhombicuboctahedron. They both consist
of eight triangles and eighteen squares (six in the planes of a cube's
faces and 12 in the planes of a cube's edges), with three squares and one
triangle meeting at each of the 24 vertices. They have the same topological
structure.
The same 45 degree twist of one half which produces the pseudo rhombicuboctahedron from the rhombicuboctahedron produces a new non-convex polyhedron called the pseudo great rhombicuboctahedron from the great rhombicuboctahedron. This new polyhedron was first described (as far as I know) in 1994 by R. Hughes Jones (see the references).
As far as I can see from studying the uniform polyhedra, these are the only two possible examples of a polyhedron in which all faces are regular and all vertices are locally identical, yet the polyhedron is not uniform; however I know of no simple proof of this.
The duals to these two pseudo polyhedra are also interesting. In each case, because the 24 vertex figures are identical, the dual consists of 24 identical faces, but there are two possible arrangements for the faces. The dual to the rhombicuboctahedron is the trapezoidal icositetrahedron. Notice that its "equators" are regular octagons, so one half can be rotated 45 degrees relative to the other, giving the dual to the pseudo rhombicuboctahedron, which I suppose must be called the pseudo trapezoidal icositetrahedron. Analogously, the dual to the great rhombicuboctahedron is the great trapezoidal icositetrahedron, which has 8/3 star octagons for its "equators." Rotating one half 45 degrees relative to the other gives the pseudo great trapezoidal icositetrahedron. (VRML pseudo models to come soon.)