Zometool Polyhedra

    The Zometool (officially Zome System) is a plastic construction set which lets you quickly and easily build edge models of many complex polyhedra. (A link to the manufacturer is at the bottom of this page.) Building your own is the best way to really understand anything and Zometool models can go far beyond what you can build as paper models. Note that the actual 3D models are much clearer than the 2D images on this page might suggest, since here you are seeing the front and rear superimposed.

    Any structured construction set has certain advantages and disadvantages. For example, there are only certain angles and lengths built in to the Zometool, so certain objects can not be constructed. On the other hand, the edges and angles available have been very cleverly designed as the symmetry axes of the icosahedron/dodecahedron. The range of things which can be built with edges in these directions is quite amazing and far beyond any other construction set I know. Furthermore, the structured design of the parts guides you into making things that you didn't know you could make.

    The basic struts (edges) come in three colors, and each color comes in three lengths. Red edges are parallel to 5-fold axes, yellow edges are parallel to 3-fold axes, and blue edges are parallel to 2-fold axes. The struts and the connector holes have 5, 3, and 2 sides to make this work out automatically. The lengths are scaled by the golden ratio so that if you make a pentagon of one size strut, the next larger size can fit in as its diagonal. In getting to know the set, this all becomes very natural. One tip is worth emphasizing however: Get in the habit of pushing the struts completely into the nodes or later your larger models will fall apart.
     
     
    The icosahedron and dodecahedron are natural projects to begin with. In a few minutes anyone can build one, regardless of prior geometric experience. You can either build them directly, or use a two-step process for your first time. The two-step process to build an icosahedron starts with you putting a red strut into all twelve 5-sided holes of one ball. Balls placed at the ends of these red struts are the twelve vertices of an icosahedron. You then connect these to each other with blue struts. Having done this once, you will find it easy to build just the icosahedron edges without the central red scaffolding the next time. 

    (Incidentally, if you look at an icosahedron with internal red struts, you see that a solid icosahedron can be dissected into twenty solid tetrahedra which meet at its center. Note however that the tetrahedra are not regular tetrahedra as some people erroneously assume. The fact that some edges are red and some are blue should make clear that they are not all the same length.)

    The two-step process for the dodecahedron is analogous, but start with twenty yellow struts in the center ball to locate the twenty vertices of the dodecahedron. Again, after doing this once, it is easy to eliminate the scaffolding and directly build just the dodecahedron the next time you do it.
     
     
    With soon-to-be-unveiled green struts, the regular tetrahedron and octahedron are also constructible. You can also make many irregular tetrahedra and octahedra. The tetrahedron shown is one twentieth of the icosahedron built above. The octahedron in the middle has eight identical faces, but they are isosceles, not equilateral. The octahedron at right has two equilateral faces and six isosceles.

     
    The remaining Platonic solid, the cube, is borderline buildable with Zometool. Just make a square from blue struts, and your cube will arise naturally. However, careful observation reveals that this is not the familiar cube which it mimics. A real cube has three axes of 4-fold symmetry, whereas the Zometool connector nodes do not allow true 4-fold symmetry. This is really a "pseudo-cube" with tetrahedral symmetry and only three mirror planes (not nine as in a real cube). The orientation of the blue edges has two up and two flat in each square, so each square really has only 2-fold symmetry. This may seem like a minor subtlety, but the whole point of the Zometool is really to understand symmetry axes, so it is worth pausing to observe that this cube (and the octahedron) does not have true 4-fold symmetry.

     
    While you are making the Platonic solids, it is a good exercise to build a model of a cube inscribed in a dodecahedron. (It is clearer in person that this photo suggests.) Either start with a dodecahedron and add one diagonal to each face, or start with a cube and add the dodecahedron's edges as a kind of "roof" on each side. The cube edge is a diagonal of the pentagon, so it is the golden ratio times as long, i.e., the next longer size blue strut.

    For a project to illustrate duality, construct a compound of an icosahedron and a dodecahedron which cross each other at their midpoints. You can do it with the dodecahedron edge being two short struts and the icosahedron edge being two medium struts.
     
     
    Among the Archimedean solids, five with icosahedral symmetry can easily be constructed using only blue struts.  Six more can be made with the green struts.  (The snub icosidodecahedron and snub cube are not Zometool-constructible as their edges are not parallel to symmetry axes.) At right is the truncated icosahedron, sometimes known as a soccer ball, or buckeyball.

     
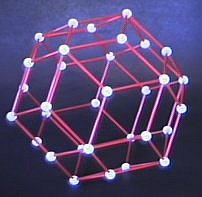
    Here is a rhombicosidodecahedron. This is the same general shape as the Zometool connector ball. If you use two sizes of struts, stretching the squares into rectangles and enlarging the triangles, you can make a large model of the Zometool ball

     
    Here is a truncated icosidodecahedron with Chris included for scale. Other Archimedean solids you can make are the truncated dodecahedron and the icosidodecahedron.

     
    All four Kepler-Poinsot polyhedra can be made. Here are versions of the small stellated dodecahedron, and the great dodecahedron and the great stellated dodecahedron.

     
    Among the Archimedean duals, two are Zometool constructible. The rhombic triacontahedron practically builds itself if you work with red struts of one length and build rhombuses. Just remember that three obtuse angles meet at some vertices and five acute angles meet at the other vertices. After you complete it, add short blue diagonals to each rhombus to see how the dodecahedron is inscribed in a rhombic triacontahedron. Or instead add long diagonals to each rhombus to make an icosahedron inscribed in the rhombic triacontahedron.

     
    The second Archimedean dual which you can make is the rhombic dodecahedron. Analogous to the cube above, this is really a "pseudo-rhombic dodecahedron" without true 4-fold symmetry if you look closely. Try adding blue struts as the short diagonal of each face, to see how a cube is inscribed in the rhombic dodecahedron. Or add green struts as the long diagonals to see the octahedron inscribed in it. Being a space-filling polyhedron, you can extend your rhombic dodecahedron model with more copies of itself which fit face-to-face and fill all space without gaps.

     
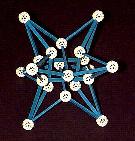
    The above two Archimedean duals happen to be zonohedra. Many other zonohedra can be constructed with the Zometool, as long as their edges are parallel to the some of the 31 axes of symmetry of the icosahedron. For example, this rhombic enneacontahedron is based on the 3-fold axes of the icosahedron.

    Many other zonohedra based on the icosahedral symmetry axes can be constructed with the Zometool. For example, try making a (red and yellow) 16 zoner, a (red and blue) 21 zoner, or a (yellow and blue) 25 zoner The ultimate is the compete 31-zone zonohedron based on all the icosahedral axes.
     
     
    After mastering zonohedra, you might like to try some of my zonish polyhedra. Victoria is resting at right, eating an apple, inside a structure she just made.
    And Colin can be seen at left, inside a zonish structure he built.

     
    Next we come to stellations. Here is a very nice one of the tetrahedral stellations of the dodecahedron. This one is especially interesting because it can fill space if you alternate it with regular dodecahedra. If you think of the model of a cube in a dodecahedron above as a cube with six roofs attached, then this is the same cube with the same six roofs subtracted from its interior.

     
    The real fun of the Zometool is that it lets you doodle in three-space. Here is one example, but if you have made many of the above, I am sure you have already many of your own doodles. This structure is based on the dodecahedron, but each edge is replaced by two yellow struts which make an outward pointing "V".

    Going beyond three dimensions to four, a wonderful model is this projection of the 4-dimensional 120-cell into 3 dimensions. Pictures of a wire model of this structure, made by Paul Donchian, can be found in Coxeter's Regular Polytopes and in Banchoff's Beyond the Third Dimension. You have to see it or make it yourself to really appreciate it. Start with a medium-sized dodecahedron as its core; the result is about 1 meter in diameter:

    Details on all the above, lots more new examples, and lots of real geometry (lengths, angles, volumes, theorems, etc.) are now available in our comprehensive book:
     

      Zome Geometry
      George W. Hart and Henri Picciotto
      Key Curriculum Press, 2001
         
    The book and the Zome kits can both be ordered from either the Zome Corporation or Key Curriculum Press. You can also try internet toy sellers like Amazon.

    Many of the models above were made by 8-, 10-, and 12-year-old Victoria, Colin, and Christopher.
    Virtual Polyhedra, (c) 1997, 1999 George W. Hart