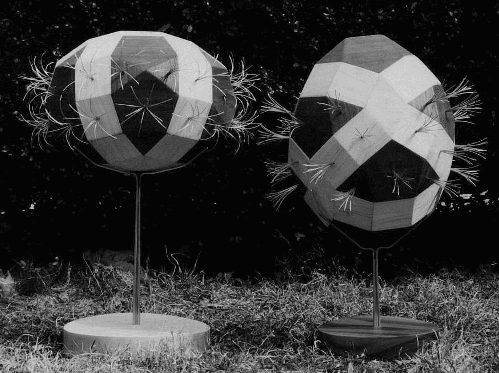The following is a webified version of: George W. Hart, "Zonish Polyhedra," Proceedings of Mathematics and Design '98 San Sebastian, Spain, June 1-4, 1998, p. 653.

ZONISH POLYHEDRA

George W. Hart

A previously unexamined class of geometric forms is presented which provides a rich storehouse of interesting designs and structures, e.g., for sculpture. They can be called "zonish polyhedra" because they have "zones" and include zonohedra as a special case, but generally are not zonohedra. A zonish polyhedron is the Minkowski sum of a "seed" polyhedron and a set of line segments. Unlike zonohedra, these polyhedra may be chiral and may have faces with an odd number of sides, e.g., triangles and pentagons.

1. Introduction

This paper presents a class of polyhedra which I do not believe has been examined before. They provide a rich source of interesting designs and structures, and are relatively easy to construct or to generate by a simple algorithm. For lack of a better term, my working name is "zonish" because these have zones, and include zonohedra as a special case, but generally are not zonohedra. Suggestions for a better term are welcome.


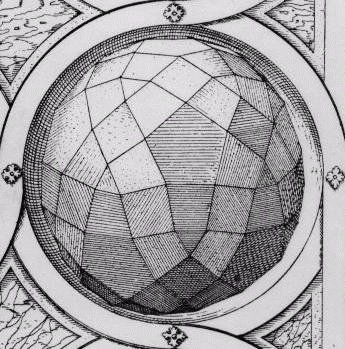
Fig. 1a. Zonish polyhedron based on icosidodecahedron, with six zones.	Fig. 1b. Drawing by Jamnitzer, 1568

Zonohedra are notable for encompassing a large diversity of forms with a small inventory of components, [1,2,3,4] but zonish polyhedra allow even more diversity, and new design possibilities, e.g. architectural. Although the zonohedra form a subset of this class of zonish solids, it is a small proper subset. As Fig. 1a indicates, zonish polyhedra may have faces with an odd number of sides, e.g., triangles and pentagons, which are not possible in zonohedra. This example consists of 122 faces: 12 pentagons, 20 triangles, 60 squares, and 30 golden rhombi (arranged as in the rhombic triacontahedron). It is an icosidodecahedron enlarged by the addition of six (light colored) zones. Zones are "equatorial" bands of faces which share a common edge direction, their zonal direction. Fig. 1b shows a similar structure, drawn by Wentzel Jamnitzer in 1568, discussed below.

2. Construction

The key idea of zonish polyhedra is a generalization of the well known method of constructing a zonohedron in which one zone is added at a time to a smaller zonohedron, starting from a point or a parallelepiped. The only difference is that here we allow any polyhedron to be a "seed" for the process. So a zonish polyhedron is characterized by a convex seed polyhedron (oriented in space) and a set of zonal direction vectors (a "star") which is used to expand the seed. If the seed is a zonohedron, the result is again a zonohedron, but when the seed is not a zonohedron, new "zonish" polyhedra are formed.


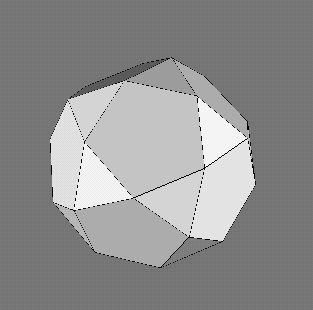
Fig. 2a. Seed	Fig. 2b. One zone	Fig. 2c. Two zones

To illustrate the process, we begin with an icosidodecahedron as seed, (Fig. 2a) and add one zone in a direction parallel to a 5-fold axis. The zonal edge length was chosen to be equal to the seed edge length so the ten new faces are squares rather than rectangles. The result (Fig. 2b) is a "Johnson solid," known as elongated pentagonal gyrobirotunda. It is formed by splitting the seed into two hemispheres and reconnecting them by inserting edges parallel to the chosen zonal edge direction. The general process is to divide a polyhedron's faces into two groups, according to whether their outward normal has a positive or negative component in the direction of the chosen zonal direction. One half is then translated by the zonal displacement vector. Where edges were separated, a new parallelogram face is inserted, joining the cut edge with vectors in the zonal direction. Convexity is always preserved.

Adding a second zone along the direction of a second 5-fold axis gives a result with two zones. (Fig. 2c) Two opposite faces, where the two zones cross, are golden rhombi. The addition of a third zone can be done in two ways. If the three zones all border some triangle, we get an oblate result. Otherwise, we get a prolate result. A sculpture which illustrates the two possibilities appears in Section 5 below. Continuing until zones are constructed for all six axes of 5-fold symmetry gives the six-zone result of Fig. 1. Note that the final construction depends only on the seed and the set of zonal vectors, not the order in which they are used.

The complication not yet mentioned is that some faces may be parallel to the zonal direction, so that the outward normal has a component of zero in that direction and does not belong to either hemisphere. In that case, that face itself must be expanded in the zonal direction, i.e., edges in contact with one hemisphere are separated from edges in contact with the other, and two new edges in the zonal direction are inserted. Thus, an n-gon (of the seed or a previous expansion step) parallel to the zonal direction appears as an n+2-gon. This is illustrated below.

In sum, a zonish polyhedron is is the Minkowski sum of the seed and a set of line segments. Faces from the seed which are not parallel to any segments remain unchanged; faces from the seed parallel to k segments are expanded to have 2k additional edges; and for every coplanar set of segments, there are two opposite centrally symmetric faces.

3. Examples

As a second case, analogous but with octahedral symmetry, begin with the cuboctahedron and expand with four zones in the directions of the axes of 3-fold symmetry. The result is a pleasing pentacontahedron (Fig. 3) consisting of 8 triangles, 30 squares, and 12 square-root-of-two rhombi (arranged as in the rhombic dodecahedron). A picture of it (not with this method of construction) appears in two books of Peter Pearce [8, p. 49] and [9, p. 50].


Fig. 3. Four-zoned cuboctahedron	Fig. 4. Ten-zoned icosidodecahedron

The above examples are special in that they begin with quasi-regular polyhedra and expand in directions orthogonal to their equatorial polygons. As a consequence they are also equivalent to Alicia Boole Stott's method [2] [4] of "expansion" of the seed polyhedron (or their dual rhombic polyhedra). If one applies either that method or the zonish expansion (along the three 4-fold axes) to the remaining convex quasiregular polyhedron, the octahedron, the result is the rhombicuboctahedron, yet another zonish polyhedron. However, in most cases, zonish solids and Stott's expansions are very different. The zonohedral expansion is essentially geometric, while Stott's expansion operation is essentially topological and does not change existing faces.

For another comparison, begin again with the icosidodecahedron, but choose ten zonal directions parallel to its ten three-fold axes of symmetry. The result (Fig. 4) is similar to Figs. 1 and 2 in that the original 32 faces of the seed are still present. But it is different in that now the zones consist of 60 hexagonal faces and 30 rhombi. The hexagons arise where a zonal direction is parallel to a face of a previous expansion step.


Fig. 5. Ten-zoned icosahedron	Fig. 6. Six zoned dodecahedron

Figs. 1 and 4 display full icosahedral symmetry, because the seed and the zonal directions do. In general, this is a strategy for producing zonish polyhedra with any desired symmetry. As two further examples of this idea, expand the icosahedron along its ten directions of 3-fold symmetry to get Fig. 5, or expand the dodecahedron along its six directions of 5-fold symmetry to get Fig. 6. The latter is equivalent to truncating the rhombic triacontahedron at its 5-fold vertices. (Casually, it might be confused with the truncated icosahedron "soccer ball". However, note that the 30 hexagons (not 20) lie in equatorial zones, they each touch two (not three) pentagons, and they are not regular hexagons.)

Figs. 1-6 are all reflexible and centrally symmetric, but that is not an essential property of zonish polyhedra (unlike zonohedra). As an example, we begin with a chiral seed, the snub dodecahedron, and expand it along its six axes of 5-fold symmetry to obtain the chiral result shown in Fig. 7. The pentagons of the seed snub dodecahedron are not separated from their adjacent triangles by the zones.


Fig. 7. Ten-zoned snub dodecahedron	Fig. 8. Ten-zoned decagonal prism

There is a certain aesthetic appeal to objects with a high degree of symmetry, yet examples with lesser symmetry are easy to construct as well. Zonish polyhedra with no symmetry can be constructed from any seed using a randomly chosen set of zonal directions. Fig. 8 illustrates a nice rosette effect which can result when the seed and star share prism symmetry. A decagonal prism was chosen as seed and it was expanded with ten zones based on the vectors from the center to the vertices of the seed.

The above examples and more are available on the internet [5] in the standard format for virtual reality format files. Any web user with a standard viewer can see them as three-dimensional objects. They can be rotated and otherwise manipulated on the screen for a clear appreciation of their structure.

4. Algorithm

An algorithm for constructing arbitrary zonish polyhedra, implemented in Mathematica, is available from the author. It operates as sketched in Section 2 above, categorizing faces according to the sign of their projection of their outward normal onto a given zonal direction, separating the hemispheres, and inserting a connecting zone of new faces. When faces are found to be parallel to a zonal direction, they are expanded from k sides to k+2 sides appropriately. Tested on a wide range of seeds and stars, it has been found to be very robust. The most difficult issue is that for very complex models, floating-point roundoff errors can make it difficult to determine if a face plane is parallel to a zonal direction. In such cases, accurate vertex coordinates for the seed must be available.

The program takes as input any seed polyhedron, specified as a virtual reality file. Currently there are over one thousand different polyhedra available in this format available in [5]. The program allows the user to specify arbitrary zonal directions, or it can extract the vertices, face centers, edge midpoints, and/or other landmark points from the seed data file. Output is in the form of another virtual reality file, so the result can be viewed in a 3D viewer.

The examples in this paper are all constructed by this program within a few seconds. Larger examples, with thousands of faces, are constructed within one minute. The images in this paper are screen captures from the CosmoPlayer 3D viewer plugin to Netscape, converted to greyscale in an image processing program.

5. Sculpture

Part of my interest in zonish polyhedra lies in the fact that they provide an infinite storehouse of engaging geometric forms. Despite their variety and straightforward derivation, I have not observed any previously illustrated examples of this class, with the exception of Fig. 3 as cited above. Interestingly, a close example appears in the work of a great artist of polyhedra, Wentzel Jamnitzer (1508-1585). Jamnitzer was a goldsmith and jeweler of the German renaissance who designed intricate conceptual monuments based on polyhedral structures. His visionary masterpiece Perspectiva Corporum Regularium contains a wide variety of designs which anticipate later mathematical discoveries, e.g., the great stellated dodecahedron, the great dodecahedron, and the rhombic triacontahedron. I was surprised recently to discover in it Fig. 1b above, very similar to Fig. 1a. They are topologically equivalent, and differ geometrically mainly in that the squares of Fig. 1a are realized as trapezoids in Fig. 1b. (The illustrations in Jamnitzer's book are engravings executed by Jost Amman from drawings by Jamnitzer. Thus, some references credit the illustrations to Amman, but the intellectual content of their design is Jamnitzer's work.)

In my own sculpture, [6] I have found that zonish polyhedra can provide inspiration or novel design solutions. Fig. 9 is a two-part sculpture of mine, Fat and Skinny, constructed of walnut, maple, and brass, 0.6 m high including the bases. Each is constructed of the identical components: 12 regular pentagons, 30 squares, 20 equilateral triangles, and 6 golden rhombi. They are each three-zone expansions of the icosi-dodecahedron, based on three of the six 5-fold axes. As mentioned in Section 2 above, there are two ways to choose three of the six axes, leading to two very different forms. The darker wood indicates the seed and the lighter wood the zones. Each has a 3-fold axis of symmetry, which is vertical as they rest in their stands. A circumferential band of six pentagons, twelve triangles, and twelve squares displays a spray of brass "cilia" in each.

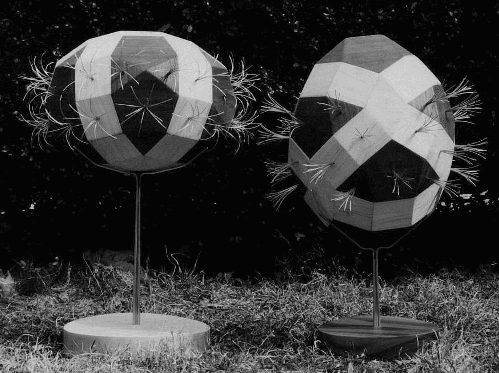Fig. 9. Fat and Skinny, by the author; walnut, maple, and brass

Fig. 10 shows another sculptural application of zonish polyhedra. This is a mobile of mine, No Picnic, currently hanging in the Hofstra University student center (variable dimensions, up to 5m in length; the largest ball is 0.8m diameter). From left to right, the three orbs are made of 240 plastic forks in six colors, 150 plastic knives in three colors, and 180 plastic spoons in six colors. Two are based on zonish polyhedra. The arrangement of forks follows Fig. 1a, with one fork for each of the 240 edges, one color per zone. The arrangement of spoons follows Fig. 5, with one spoon for each of the edges, except those meeting at the 5-fold vertices.

Fig. 10. No Picnic, by the author; plastic tableware mobile, up to 5m in length

A close-up image of the fork component, focused on one of the twelve points of 5-fold symmetry appear as Fig. 11. At each such point, five of the six colors meet. Opposite points have the same set of colors, but in the opposite cyclic order. A closer image of the spoon component is given in Fig. 12. It can be seen as a set of twelve 15-gonal cycles, each in a solid color, weaving through each other. Parallel cycles are a common color, so six colors are used.


Fig 11. Fork component of above mobile	Fig. 12. Spoon component of mobile

For these pieces, I sought forms with icosahedral symmetry and a certain degree of complexity. Zonish polyhedra provide a spectrum of possibilities on which to base a design and suggested a technique for engineering their assembly. For their construction, I clamped the plastic tableware pieces to each other and a jig made from a commercial polyhedral construction toy. After gluing the components together with a solvent cement, the jig could be disassembled and removed through the openings.

6. Conclusion

Zonish polyhedra offer a wide variety of attractive forms which may be applicable to a range of design problems. Computationally, they are readily constructed and visualized in three dimensions. Their use in sculpture has been illustrated.

Many nice mathematical properties have not been discussed here, for lack of space. For example, there are nonconvex and higher-dimensional analogs. There is also a relationship between a zonish polyhedron and larger zonohedron based on the same star plus all the edge directions of the seed.

Akin to zonohedra, the zonal expansion construction illustrates how zonish polyhedra can be nicely dissected. While a zonohedron can be dissected entirely into parallelepipeds, the analogous construction dissects a zonish polyhedron into parallelepipeds, prisms (based on the seed's faces) and one copy of the seed itself. This suggests some interesting puzzle toys.

References

Zome Primer

[2] Walter William Rouse Ball, revised by H.S.M. Coxeter, Mathematical Recreations and Essays, New York, 1938; 11th ed., 1960, (Dover reprint).

[3] David Booth, "The New Zome Primer," in Istvan Hargittai (editor), Fivefold Symmetry, World Scientific, 1992.

[4] H.S.M. Coxeter, Regular Polytopes, Macmillan, 1963, (Dover reprint, 1973).

[5] http://www.georgehart.com/virtual-polyhedra/zonish_polyhedra.html

[6] http://www.georgehart.com/sculpture/sculpture.html

[7] Wentzel Jamnitzer, Perspectiva Corporum Regularium, Nuremberg, 1568, (Gutenberg Reprints, Paris 1981).

[8] Peter Pearce, Structure in Nature is a Strategy for Design, MIT, 1978.

[9] Peter Pearce and Susan Pearce, Polyhedra Primer, Van Nostrand Reinhold, (reprinted by Dale Seymour Publications) 1978.