Kepler's logical approach to polyhedra does not mean that he was free of the mysticism of the day. The following illustration, from his 1619 book, Harmonice Mundi, graphically shows the Platonic associations of the regular solids with the classical elements: The tetrahedron corresponds to fire, the octahedron to air, the cube to earth, the icosahedron to water, and the dodecahedron to the cosmos or ether:
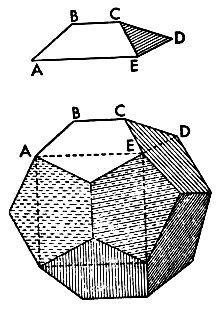
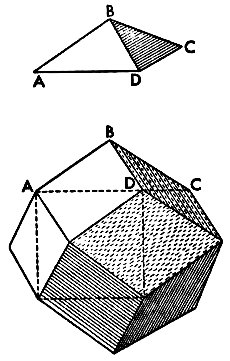
The lower-right portion of the above figure illustrates the disassembly of two rhombic solids which Kepler discovered: the rhombic dodecahedron and the rhombic triacontahedron. (An illustration of an approximation to the triacontahedron is clear in one of Jamnitzer's monuments drawn fifty years earlier, but Kepler certainly had a much deeper understanding of the triacontahedron's structure and its relationships to other polyhedra.) Below, left, Kepler shows how a dodecahedron can be constructed by adding "roofs" to the six sides of a cube (the construction which Euclid uses). Below, right, is how Kepler constructs a rhombic dodecahedron analogously. These figures are from his book Epitome of Copernican Astronomy.
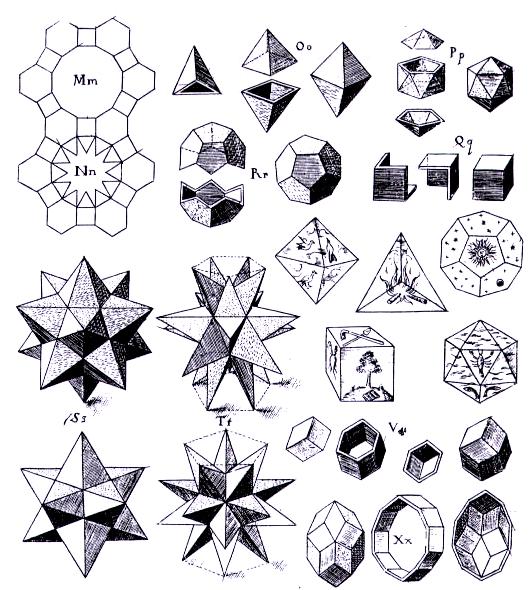
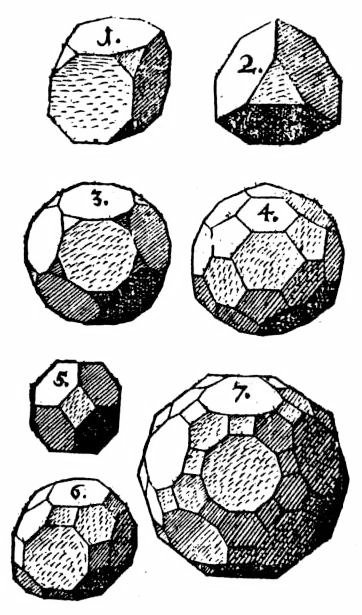
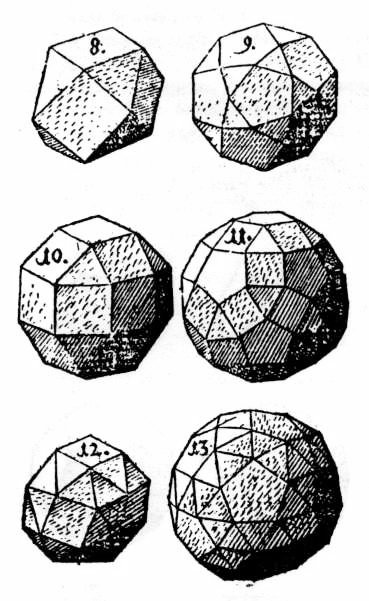
In, Harmonice Mundi, Kepler also defined the class of convex uniform polyhedra which we call the Archimedean solids, unfamiliar with the fact that Archimedes had defined the class already. All of these polyhedra except one (the snub dodecahedron, number 13 at the bottom right below) had already appeared in the work of various Renaissance artists. But those artists were haphazard, and wrote as if there could be an infinite number of related polyhedra which they were selecting from. Kepler's important contribution was to define this class of polyhedra and systematically explore it, to find all its members and prove his set was complete. In doing so, he realized that the prisms and antiprisms belong to the same class, since at each vertex the same combination of regular polygons meet.
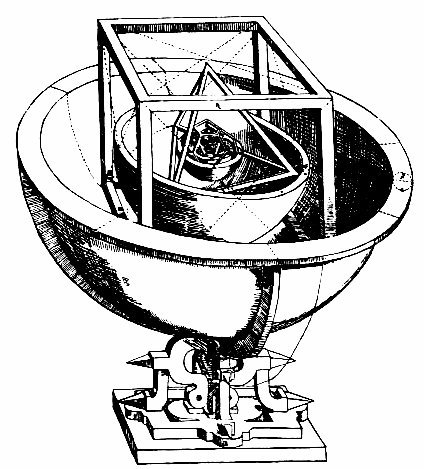
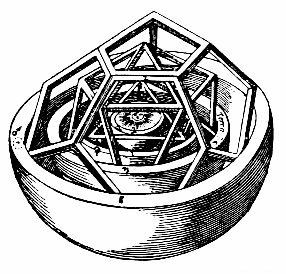
The image at right is a closeup of the spheres of inner planets, Mercury, Venus, Earth, and Mars. This is a beautiful astronomical model. For example, it explains why there are only six planets: How could there be a seventh planet, when Euclid proved that there are only five Platonic solids! Of course, the model is completely false, the interplanetary distances it predicts are not sufficiently accurate, and Kepler was scientist enough to accept this eventually. But it an excellent example of how truth and beauty are not always equivalent.