Prisms and Antiprisms
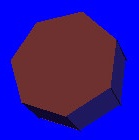 A
prism consists of two copies of any chosen regular polygon (one becoming
the top face, and one becoming the bottom face), connected with squares
along the sides. By spacing the two polygons at the proper distance, the
sides consist of squares rather than just rectangles. At each vertex, two
squares and one of the polygons meet. For example, based on a 7-sided heptagon,
is the heptagonal prism (4,4,7).
A
prism consists of two copies of any chosen regular polygon (one becoming
the top face, and one becoming the bottom face), connected with squares
along the sides. By spacing the two polygons at the proper distance, the
sides consist of squares rather than just rectangles. At each vertex, two
squares and one of the polygons meet. For example, based on a 7-sided heptagon,
is the heptagonal prism (4,4,7).
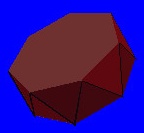 An
antiprism also consists of two copies of any chosen regular polygon, but
one is given a slight twist relative to the other, and they are connected
with a band of alternately up and down pointing triangles. By spacing the
two polygons at the proper distance, all the triangles become equilateral.
At each vertex, three triangles and one of the chosen polygon meet. Example:
heptagonal antiprism. (3,3,3,7).
An
antiprism also consists of two copies of any chosen regular polygon, but
one is given a slight twist relative to the other, and they are connected
with a band of alternately up and down pointing triangles. By spacing the
two polygons at the proper distance, all the triangles become equilateral.
At each vertex, three triangles and one of the chosen polygon meet. Example:
heptagonal antiprism. (3,3,3,7).
I have included models of prisms and antiprisms ranging from three sides up to ten sides in this list of prisms and antiprisms.
A special case of the prism is the cube (when the chosen top and bottom face is a square). And, a special case of the antiprism is the octahedron (when the chosen top and bottom face is a triangle).
Kepler was the first to discuss antiprisms,
and recognize the connection between prisms and the Archimedean solids.